Research on conceptual change (CC) has shown that some academic knowledge and the modes of reasoning required are particularly difficult to learn, especially for children, because they require a significant change in the students’ prior knowledge and habitual modes of reasoning for the new knowledge to be mastered. In other words, they require “CCs” in the prior knowledge and modes of reasoning. As such, “the name “conceptual change” embodies a first approximation of the primary [learning] difficulty: students must build new ideas [i.e., “concepts”] in the context of old ones, hence the emphasis on “change” rather than on simple accumulation or (tabula rasa or “blank slate”) acquisition” (diSessa, 2014, p. 88).
Most research on CC challenges in education has focused on learning scientific knowledge, particularly counterintuitive concepts. These range from knowledge of physics, such as Newtonian mechanics or how gravity holds objects to the Earth, to biological knowledge, such as the theory of evolution or genetics. For example, it is often difficult to learn the Newtonian concept of force, namely, that the force of an object is precisely its mass multiplied by its acceleration. The concept diverges from prior knowledge that students tend to have, such as the assumption that thrown objects acquire or contain an internal force. However, CC problems can apply to many types of knowledge, ranging from mathematics to social sciences (Amin & Levrini, 2018). For example, children’s preinstructional conceptions of numbers are developed in the act of counting discrete objects in everyday life and are often enriched during instructional learning via the counting properties of natural numbers (Christou et al., 2007; Vamvakoussi & Vosniadou, 2007). Therefore, children typically form a misconception that numbers have a discrete nature, which conflicts with the continuous nature of rational numbers (Christou et al., 2007; Merenluoto & Lehtinen, 2004; Vamvakoussi & Vosniadou, 2007). Thus, CC varies in nature and difficulty depending on the knowledge to be learned. It also depends on the student’s prior knowledge, age, and cognitive development, as well as their sociocultural, affective, or identity relationships with the new knowledge (Amin & Levrini, 2018; Levrini et al., 2021). The issues related to CC are among the most important in education (Vosniadou, 2007a) and the learning sciences, as they address the fundamental problems of knowledge acquisition, revision, and reorganization (diSessa, 2014; Mayer, 2002).
Research on CC has existed since the 1970s (Vosniadou, 2013). It is diverse and includes competing theories on the nature, constituents, and underlying mechanisms of CC. I do not defend any particular theory here. Rather, I explain their convergences and differences. Despite the divergences, researchers have accumulated recurrent findings on the systematic learning difficulties related to CC that students, especially children, face in education. Thus, research has converged to identify some of the challenges in education in this regard. In response, different research trends have suggested educational recommendations. While designing educational methods to address CC challenges is a central aim of CC research, it is an area of research that still requires refinement (Levrini et al., 2021; Treagust & Duit, 2008; Vosniadou, 2019), and researchers do not agree on which educational methods should be preferred (diSessa, 2014). This lack of consensus is due to competing theories about the nature of CC that lead to a preference for some strategies over others. It is also due to the heterogeneity of school subjects, types of knowledge, types of learners, and aspects of CC (from cognitive to sociocultural factors). This diversity precludes a single set of educational methods from addressing all the challenges that issues of CC impose on education.
However, I show in this paper that one set of educational approaches is promising for addressing CC challenges but is absent from CC literature: developmental teaching (DT) approaches, ranging from El’konin-Davydov’s developmental education (Davydov, 1972/1999, 1988/2012) to Gal’perin’s (1957/1989b, 1978/1992) method of stage-by-stage formation of mental actions and concepts. DT approaches are derived from Vygotsky’s research on how the systematic learning of academic knowledge can foster conceptual development (Karpov, 2003). They are specifically designed to develop the mastery of academic knowledge in order to foster conceptual development, including by overcoming the CC challenges. The available evidence on their results is encouraging (Arievitch & Stetsenko, 2000; Chudinova, 2019; Davydov, 1972/1999, 1988/2012; de Araujo et al., 2020; Ferreira, 2005; Gordeeva, 2020; Hedegaard & Lompscher, 1999; Karpov, 1995; Karpov & Bransford, 1995; Karpov & Haywood, 1998; Lantolf et al., 2020; Rubtsov & Ulanovskaya, 2020; Venenciano et al., 2021). This is the first paper to systematically address the connections between CC research and DT research. These research paradigms have evolved without interacting with each other, despite shared interests in theories of CC and related educational design. To overcome this lack of interaction, I delineate convergences and divergences between DT research and three CC research trends: framework theory, ontological theory, and knowledge-in-pieces theory. This enables me to conclude the paper by suggesting a series of articulations between DT research and CC research in general and the three CC research trends in particular.
The first section of the paper presents the main CC learning challenges in education, followed by the recommendations for fostering CC from the three main trends in research on CC and education: framework theory, ontological theory, and knowledge-in-pieces theory. The second section of the paper presents DT approaches and how they address the CC challenges in education. I delineate (a) convergences and divergences between DT research and the three CC research trends and (b) specificities of DT approaches, both concerning theories of CC and educational recommendations to foster CC. I also provide examples of DT lessons on bodies of knowledge typically addressed in CC research: the Newtonian concept of force, the concept of real number, and the theory of evolution. I conclude this section with a brief review of the evidence of the recurring positive learning outcomes of DT approaches. The paper concludes with suggestions for articulations between CC research and DT research.
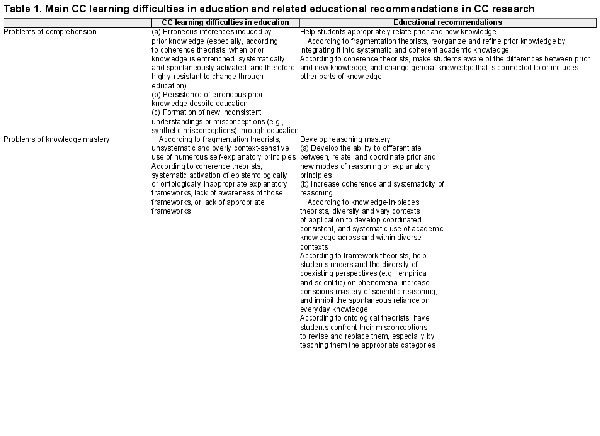
CC Learning Difficulties in Education
Problems of Comprehension
The Binding Influence of Prior Knowledge that Leads to Erroneous Inferences
One of the main difficulties in learning new knowledge that requires CC is the binding influence of the student’s prior knowledge, including patterns of reasoning. In other words, “a student […] possesses knowledge gained prior to some formal instruction in a discipline. This prior knowledge might come from direct experience of the physical world, informal discussions with adults or other children, or prior formal instruction” (Sherin, 2018, p. 63–64). Among the types of prior knowledge, students come to school with some knowledge that they have repeatedly relied on in everyday life during recurrent perceptual experiences or cultural experiences (Chi, 2005; diSessa, 1993; Vosniadou, 1994). Preinstructional knowledge constitutes the initial explanatory resources that students rely on when learning new subject matter, which can lead to misunderstandings or erroneous inferences when it is inconsistent with this new knowledge. Most research has emphasized that this type of prior knowledge can be particularly entrenched, spontaneously activated, and sometimes so discrepant with new knowledge that students can be highly resistant to change through education (Limón & Mason, 2002; Vosniadou, 2013; Vosniadou et al., 2007). For example, when learning the astronomical concept of the Earth, children must revise some well-entrenched preinstructional knowledge from everyday perceptual experiences, such as the assumptions that space is organized around a unique and constant “vertical” direction and that any unsupported object falls (Vosniadou & Brewer, 1992).
One can only learn by building new ideas in the context of prior knowledge. Prior knowledge then plays an ambivalent role by being “both an enabler of CC – providing the building blocks out of which new knowledge structures are built – and an obstacle to CC” (Mayer, 2002, p. 110). In this regard, a central fault line in CC research concerns the nature of preinstructional knowledge (diSessa, 2013). Fragmentation theorists argue that preinstructional knowledge consists primarily of numerous ideas or explanatory principles that are relatively independent of one another as distinct pieces of knowledge; diSessa’s (1993, 2017, 2018a) knowledge-in-pieces theory stands out in this respect. By contrast, coherence theorists hold that preinstructional knowledge is mostly coherently interconnected through a series of core causal attribution and categorization relationships (i.e., it is embedded in “theories”). However, their assumed degree of coherence varies depending on the theoretical approach. Although Gopnik and Wellman’s (1994) and Carey’s (2009) theories are prominent among coherence theories, in this paper, I only refer to the two coherence theories specifically related to CC in the context of issues with education: Vosniadou's framework theory (Vosniadou, 1994; Vosniadou & Skopeliti, 2014), and Chi’s (1992, 2005, 2013) ontological theory. Vosniadou’s framework theory argues that children develop loose but relatively coherent conceptual frameworks at an early age that link together a series of presuppositions (e.g., the connected assumptions underlying children’s mental models of the flat Earth). Chi’s ontological theory focuses on the coherence of CCs related to the transition from one conceptual category to another, especially ontological categories – i.e., the nature attributed to a category of things, such as whether they are entities, processes, or mental states, and of what kind – in that it consistently determines the attribution of a set of predicates consistent with that category. An example of CC at the ontological level is the shift from an incorrect understanding of the process of biological evolution as being caused by sequential processes to a correct understanding of those processes as being caused by emergent processes (Chi et al., 2012).
From the Persistence of Old Misconceptions to the Formation of New Erroneous Understandings
Research has shown that conventional teaching is generally ill-equipped to facilitate appropriate CC across a range of topics (diSessa, 2014). In the case of comprehension difficulties, these educational shortcomings have been documented with (a) the persistence of misconceptions (Chi & Roscoe, 2002; Chi, 2013) or (b) the formation of new misconceptions or inconsistent understandings due to erroneous inferences that students draw on the basis of their prior knowledge when interpreting new information (Chi, 2013; diSessa, 2018a; Henderson et al., 2018; Vosniadou, 1994). Competing theories diverge on the nature and mechanisms of the formation of these inferential errors. For example, framework theorists have documented a type of misconception formed through education called synthetic misconceptions, which combine aspects of prior and new knowledge (Vosniadou, 1994; Vosniadou & Skopeliti, 2014). For framework theorists, synthetic misconceptions result from students’ attempts to make sense of new information by integrating it into their existing loose but coherent theoretical frameworks. This interpretation is supported by researchers’ documentation of progressive sequences in the revision of synthetic misconceptions (Vosniadou, 1994; Vosniadou & Skopeliti, 2014). These revisions initially concerned minor aspects of the original theoretical framework that they interpreted as being constrained by the need to maintain the framework’s coherence. They progressed to more significant changes, which gradually led to the complete revision of the theoretical framework. For example, when children learned the astronomical concept of the Earth, they initially started with a square, rectangle, or disk model of the Earth, and they tended to develop synthetic models of the Earth in the following order: first, a mental model of a spherical Earth coexisting with another flat Earth on which human beings live; second, a hollow sphere in space where human beings still live on a flat ground inside that sphere (this incorporates some aspects of the astronomical concept but preserves the beliefs that human beings live on flat ground and that gravity works vertically); third, a truncated sphere where people live on flat ground at its top and bottom parts (this abandons the belief that gravity works vertically but preserves the belief that people stand on flat ground); and finally, mastery of the actual astronomical model (Vosniadou & Brewer, 1992).
Research has highlighted the shortcomings of educational methods that involve the direct presentation of information for promoting CC for a range of topics or concepts (Mayer, 2002; Treagust & Duit, 2008). For example, primary school teaching of the astronomical concept of the Earth often consists of telling young children that the Earth is not flat but round like a ball and showing them a globe; this method is widespread but insufficient (Vosniadou & Skopeliti, 2014). However, research has also clarified that difficulties in facilitating CC apply differently to many types of education depending on the knowledge, learners, and methods used. For example, methods such as the use of analogies that rely primarily on students’ prior knowledge and experiences can be problematic, even though analogies are often recommended as an educational strategy to induce CC (Chi et al., 2012; Clement, 2013; Henderson et al., 2018). These methods may cause confusion between prior and new knowledge rather than facilitating a clear understanding of the latter due to erroneous similarities inferred by the student between the two (Chi et al., 2012; Clement, 2013; Henderson et al., 2018). Direct teaching of content can sometimes be more effective. For example, teaching an ontological category that students might lack can be a prerequisite for ensuring they have the right interpretive framework (e.g., explaining what emergent processes are and how they contrast with sequential processes; Chi, 2013; Chi et al., 2012; Henderson et al., 2018). Similarly, education that emphasizes students’ self-directed reasoning through discovery or inquiry over direct transmission can also be problematic for CC, particularly in science learning (Kirschner, 2009; Kirschner et al., 2006). It risks overestimating students’ abilities to understand and construct academic knowledge specific to a new and unfamiliar domain on the basis of their prior knowledge and self-directed reasoning patterns (Chi, 2005, 2013; Clement, 2013; Kirschner, 2009; Kirschner et al., 2006; Vosniadou, 2007b).
Problems of Knowledge Mastery
Other difficulties in learning knowledge requiring CC are not related to difficulties of understanding but of mastery. New academic knowledge requiring CC can rarely be mastered without first becoming acquainted with the modes of reasoning it requires (Amin & Levrini, 2018; Chinn, 2018). Research has identified the difficulties novice learners face compared to domain experts and often highlights the additional learning difficulties children face. In contrast to novices, experts have a high level of prior knowledge, experience, and mastery of the reasoning patterns necessary to adequately interpret the knowledge involved. Interpretations of the fundamental differences between novices and experts regarding the issues of CC vary between theories. Fragmentation theorists interpret them primarily as a difference between experts’ stable and systematic mastery of a highly coherent body of academic knowledge as opposed to novices’ more unsystematic and highly context-sensitive reliance on self-explanatory principles (i.e., fragmented knowledge; diSessa, 2014, 2018a). Coherence theorists highlight the ontological or epistemological presuppositions providing different explanatory frameworks between novices and experts, which are systematically activated. Framework theory and ontological theory state that novices, especially children, tend to be unaware of the assumptions that constrain their reasoning, including their ontological or epistemological presuppositions, or they lack the required modes of reasoning. These deficits concern ontological categories, according to ontological theorists (Chi, 2005; Chi et al., 1981), and the thinking patterns required by academic knowledge, such as systematic and intentional hypothesis testing, according to framework theorists (Kyriakopoulou & Vosniadou, 2020; Vosniadou & Skopeliti, 2014). Fragmentation theorists, by contrast, have criticized claims of radical differences between novices and experts or between children and adults (diSessa, 2017, 2018a; Smith et al., 1994). They have documented many situations where preinstructional, self-explanatory principles are included in or share significant similarities to expert-type reasoning and play a facilitating rather than blocking role in their realization.
Research has also shown that even when students, especially children, understand new knowledge that requires CC, they often face difficulties in mastering it. They may mix adequate modes of explanation with familiar but inadequate prior modes of explanation or may alternately and unstably rely on one and then the other depending on the context (diSessa, 2017, 2018a; Kyriakopoulou & Vosniadou, 2020). diSessa’s microgenetic studies have particularly revealed that students can switch from one explanatory principle to another depending on the context. For example, in an interview, a student was asked, “What happens when you toss a ball into the air?” (diSessa, 2018a, p. 70). She first offered a correct normative response: there is only one force, gravity, which slows the ball down. Once the interviewer asked, “What happens at the peak of the toss?” she began to reformulate her model and introduced an upward force equal to gravity that comes from the hand that overbalances gravity and reaches an equilibrium at the top, and then gravity takes over on the way down. In the next sessions, which included instructional sequences, the subject gave an almost perfect physical explanation but, after being asked subsequent questions, returned to the erroneous two-force model (diSessa, 2018a, p. 70–71). Table 1 summarizes the CC learning difficulties imposed on education.
Educational Recommendations to Foster CC
Educational Recommendations to Overcome Comprehension Difficulties
To address the challenges teachers face in facilitating CC, proponents of the different CC research trends have provided a series of educational recommendations. One of the overarching educational goals, which inspires the first set of recommendations, is to help students appropriately relate their prior knowledge to new knowledge to be learned. To this end, research converges on the need to first identify the student’s relevant prior knowledge and, according to coherence theorists, its implication for coherently interconnected causal attributions and categorization relationships. The recommendations for relating prior knowledge to new knowledge differ depending on the approach (Mayer, 2002). Fragmentation theorists favor the identification of prior knowledge and familiar patterns of reasoning that could be used productively by being refined and reorganized through their integration into new, more systematic, and coherent academic knowledge (diSessa, 2017, 2018a). In other words, this line of research focuses on building on prior knowledge to foster CC by providing continuity with the new knowledge to be learned. Returning to the abovementioned incorrect explanations of force, e.g., students see balancing at the peak of the toss. But “balancing is a rough version of an incredibly important principle in physics, conservation of energy. Similarly, the upward ‘force’ in the incorrect explanation is not absent, but it is what physicists call momentum” (diSessa, 2014, p. 89–90).
By contrast, coherence theorists have focused on making students aware of and correctly understand the differences between prior and new knowledge to further highlight their discontinuity (Chi, 2005, 2013; Henderson et al., 2018; Vosniadou, 1994, 2019). Framework theorists and ontological theorists have also insisted that education should be adapted to first change prior knowledge that constrains the CC in connected or subordinate bodies of knowledge. For example, according to ontological theory, when children make a category error, such as confusing whales with fish, education must first make them aware of this error at the categorical level (e.g., by pointing out that whales do not breathe through gills but through a blowhole) to induce a categorical change through which the conceptual and causal attributes associated with the other category can then be attributed to the concept (Chi, 2013). In science learning, categorical shifts often require helping students to overlook superficial perceptual similarities at the pattern level (Chi, 2013). As for framework theory research, to build on the example of the astronomical concept of the Earth, to make this concept understandable, education should at least start by prioritizing children’s understanding of how people can stand on Earth’s bottom and side without falling off (i.e., explain gravity) or why Earth is round even though they perceive it as flat (e.g., by demonstrating with a large round object that it can appear flat from the perspective of someone standing on it; Vosniadou et al., 2001).
Educational Recommendations to Overcome Problems of Knowledge Mastery
Mastery of new knowledge that requires CC often requires mastery of specific modes of reasoning, and students, especially children, often struggle with this. Therefore, another overarching goal, which is accompanied by another set of educational recommendations, is to develop mastery of reasoning. Two general recommendations for achieving this mastery are shared in CC research. The first is to develop students’ abilities to differentiate between, relate, and coordinate their prior habitual modes of reasoning or explanatory principles and the new academic modes (Chi, 2013; diSessa, 2017, 2018a; Kyriakopoulou & Vosniadou, 2020; Treagust et al., 2018; Vosniadou & Skopeliti, 2014). The second recommendation is to increase the consistency and systematicity of use by students (Chi, 2013; diSessa, 2017, 2018a; Kyriakopoulou & Vosniadou, 2020; Treagust et al., 2018; Vosniadou & Skopeliti, 2014). Satisfying these two recommendations for achieving mastery of reasoning contributes to refining students’ epistemologies, i.e., their conceptions of the difference of nature between their own preinstructional knowledge and the new academic knowledge. To meet these recommendations, specific strategies differ between approaches.
To increase students’ abilities to differentiate between, relate, and coordinate their prior and new ways of thinking, diSessa’s (2017, 2018a) knowledge-in-pieces theory emphasizes students confronting a variety of diverse contexts in which they learn different ways of interpreting the same concepts. This develops knowledge transfers that account for – rather than neglect – contextual variation (Wagner, 2006). Knowledge-in-pieces theory particularly emphasizes the need to develop coordinated, consistent, and systematic use across and within diverse contexts, as it considers that it is the very medium that induces CC. Framework theorists rather emphasize the development of the intentional (i.e., conscious and deliberate) metacognitive mastery of executive functions (working memory, shifting, inhibition) to increase conscious mastery of scientific reasoning and to inhibit the spontaneous reliance on everyday knowledge (Kyriakopoulou & Vosniadou, 2020; Vosniadou, 2019). Framework theorists also emphasize the importance of students understanding that their prior modes of reasoning are not false but are only one perspective (e.g., an empirical perspective) among others (e.g., scientific perspectives; Vosniadou, 2019; Vosniadou & Skopeliti, 2014). Ontological theorists focus on students confronting (directly or indirectly) their misconceptions to help them revise and replace them (Chi, 1992, 2005, 2013). They assume that most or all preinstructional knowledge impedes CC because it is misconceived or lacks accurate categories. Thus, they privilege directly teaching the new categories to master the type of reasoning required. Table 1 summarizes the general educational recommendations from the three CC research trends.
DT Approaches and Their Promising Role in Addressing the Challenges of CC in Education
DT approaches emerged from research by Russian psychologists working closely together during the Soviet era (Karpov, 2003). Among them were psychologists A.N. Leontiev, A.R. Luria, P. Ya. Gal’perin, V.V. Davydov, D.B. El’konin, N.F. Talyzina and philosophers S.L. Rubinstein and E.V. Ilyenkov. Two DT approaches emerged from this educational research tradition. The first is Gal’perin’s (1957/1989b, 1978/1992) method of stage-by-stage formation of mental actions and concepts, which continues to be refined and advocated for (Arievitch & Haenen, 2005; Arievitch & Stetsenko, 2000; Arievitch & van der Veer, 1995; Engeness, 2021; Engeness & Lund, 2020; Haenen, 2000, 2001; Karpov, 2013; Karpov & Haywood, 1998; Karpov & Kozulin, 2018; Kozulin et al., 2003; Lantolf & Poehner, 2014). The second is El’konin-Davydov’s developmental education, which was refined by Davydov (1972/1999; 1988/2012) and also continues to be refined and advocated for (Aidarova, 1982; Chaiklin et al., 1999; de Araujo et al., 2020; Engeström et al., 1999; Hedegaard, 1996; Hedegaard & Chaiklin, 2005; Hedegaard & Lompscher, 1999; Kozulin et al., 2003, 2018; Markova et al., 1974/1979; Schmittau, 2004; Venenciano et al., 2021; Zuckerman, 2004). However, DT approaches also include the research led by El’konin (1989) and Talyzina (1975/1981). DT approaches share a series of educational principles and methods (Arievitch & Stetsenko, 2000; Davydov, 1972/1999; Karpov, 2013; Karpov & Bransford, 1995; Karpov & Kozulin, 2018; Kozulin et al., 2003). Sometimes referred to as (Neo-)Vygotskian approaches to teaching (e.g., Karpov & Kozulin, 2018), DT approaches are indeed a continuation of Vygotsky’s research on how instruction can improve psychological development (hence the name DT), especially how the systematic learning of academic concepts can significantly change children’s preinstructional knowledge, reasoning, and comprehension skills by improving their conceptual development (Karpov, 2003).
DT approaches are absent from the research literature on CC and education. Although few DT researchers referred to CC literature (e.g., Giest & Lompscher, 2003; Haenen et al., 2003; Hedegaard, 1996; Kozulin, 2003), CC issues are central in Vygotskian and DT theories and educational approaches (Bozhovich & Zinchenko 1941/1979; Davydov, 1972/1999; El’konin, 1963/1999; Gal’perin, 1969/1989a; Kozulin et al., 2003; Margolis, 2020). In this section, I argue that DT approaches are promising for addressing CC challenges. I interpret how CC, CC problems, and educational recommendations to foster CC can be viewed from a DT perspective. I delineate (a) convergences and divergences between DT research and the three CC research trends and (b) specificities of DT approaches. I also provide examples of DT lessons on the Newtonian concept of force, the concept of real number, and the theory of evolution. I conclude this section with a brief review of the evidence of the recurring positive learning outcomes of DT approaches.
Theory of CC in Education from a DT Perspective
According to Vygotsky (1934/1987), academic or scientific concepts are understood in a broad sense, not limited to the natural sciences, as a set of abstract, precisely defined features, and relations linked systematically to one another and to other concepts by objective and causal-logical relations, especially relations of generality. In contrast to academic concepts, concepts formed in everyday life during recurrent cultural and empirical experiences – i.e., “everyday” or “empirical” concepts – tend to be rich in personal and concrete experiences, less precise and fixed, used spontaneously and without reflection, and mostly used without being based on systematic causal-logical relationships. Vygotsky hypothesized that the mutual discrepancies between academic and everyday knowledge make it difficult for students to establish appropriate relationships for mastering academic knowledge, especially for children; however, these discrepancies also allow for important CCs through systematic education. Vygotsky and DT researchers rejected the views that preinstructional empirical knowledge and academic knowledge are antagonists and that academic knowledge must replace preinstructional empirical knowledge. Indeed, they considered that preinstructional empirical knowledge is not wrong or misconceived (contrary to ontological theory) but valid in certain contexts and for certain cognitive goals and types of understanding (Arievitch & Stetsenko, 2000; Davydov, 1972, 1999; Gal’perin, 1969/1989a), in line with framework theorists and especially fragmentation theorists.
Vygotsky assumed that academic concepts become meaningful and concretized when one reflects on everyday concepts and integrates them into their well-defined system of explanations and generalization. The CCs that result, for Vygotsky (1934/1987) and DT researchers, range from significant changes in systematicity, coherence, and precision, including higher levels of generalization and abstraction, to radical changes in understanding (Davydov, 1972/1999; Gal’perin, 1969/1989a). The latter include: (a) discovering systematically interrelated essential properties of a series of objects, phenomena, or events and (b) thinking systematically and independently on the basis of these essential properties. This independent thinking is related to an increase in intentional metacognitive mastery when learning academic knowledge (Davydov, 1972/1999; de Araujo et al., 2020; Vygotsky, 1934/1987). Metacognitive mastery is considered important for reasons similar to those of framework theorists: because it increases awareness of one’s own thinking processes and the control over spontaneous reliance on everyday knowledge. Thus, Vygotsky opened a line of research focusing on the potential of instruction to foster significant CCs, especially in children, which DT researchers continued.
DT researchers consider that the specificity of academic concepts, which they call theoretical concepts, is the theoretical mode of thinking their content requires: to explain – via specific causal-logical relationships – the origin, genesis, and functioning of various concrete phenomena or objects based on a core set of properties systematically interrelated (Arievitch & Stetsenko, 2000; Davydov, 1972/1999). For instance, the theoretical concept of life in biology is based on the core interrelation between an organism and an environment, which enables one to explain theoretically the diversity of biological phenomena (Ilyenkov, 1960/1982). This view of academic knowledge contrasts with Vygotsky’s emphasis on abstract classificatory relations of generality and his lack of attention to theoretical mental methods of analysis (Davydov, 1972/1999; Karpov, 2003). DT researchers developed educational approaches that aim to develop theoretical thinking in every school subject to foster students’ conceptual development, including by overcoming CC challenges (Davydov, 1972/1999; Gal’perin, 1969/1989a).
Vygotsky is particularly known for his hypothesis that higher psychological processes (e.g., the ability to think with academic knowledge) emerge from social interactions in societal practices (for details, see Chaiklin, 2015). However, the sociocultural and interactional levels were of interest to Vygotsky (1934/1987) and DT researchers to the extent that they are translated, via an internalization process, into individual mental processes and capacities (Davydov, 1972/1999). For instance, DT researchers emphasized that specific types of school education (types of learning and teaching, cognitive operations performed, contents and materials involved, educational interactions) inform specific cognitive developments. Yet, many research trends appropriated Vygotskian theories by prioritizing the sociocultural or interactional levels over – and often at the expense of – the individual mental level, including: (a) social constructivist education (Amineh & Asl, 2015; Palincsar, 1998), (b) situated cognition approaches of Lave and Wenger’s (1991) community of practice theory or of Rogoff’s (1990) learning by apprenticeship theory, and (c) the self-proclaimed third and fourth generations of cultural-historical activity theory (Engeström & Sannino, 2020).
The Reasons for the CC Learning Difficulties from a DT Perspective
DT approaches were significantly designed on the basis of analyzing students’ typical learning difficulties in school, especially those of children, including CC problems (Arievitch & Stetsenko, 2000; Davydov, 1972/1999; Gal’perin, 1969/1989a, 1978/1992; Karpov, 2003). Although DT researchers did not use the following terms, they found evidence about the persistence of misconceptions and the formation of new misconceptions or inconsistent understandings, including sequences of progressive CCs and what framework theorists call synthetic misconceptions, as well as miscategorizations of the types studied by ontological theorists (Davydov, 1972/1999, Gal’perin, 1969/1989a). DT researchers also documented the unstable or insufficient mastery of modes of thinking that require CC in different subject domains, including mixing preinstructional and academic modes of explanation, alternately relying on one and then the other, or relying unsystematically on the adequate mode of reasoning depending on the context (Davydov, 1972/1999).
DT researchers considered that these learning problems arise because of educational approaches that fail to develop theoretical thinking and because preinstructional empirical knowledge negatively influences learning (Davydov, 1972/1999; Gal’perin, 1969/1989a, 1978/1992). They assumed, like ontological theorists, that one empirical thinking tendency, in particular, impairs CC: the spontaneous tendency of students, especially children, to rely on superficial perceptual features, particularly salient and visual features, in contrast to relying on essential properties (Davydov, 1972/1999; Gal’perin, 1969/1989a). Thus, DT researchers emphasized: (a) the qualitative differences between prior and new knowledge, (b) a systematic and negative influence of a few preinstructional thinking tendencies on CC, and (c) students’ lack of adequate modes of thinking. DT researchers’ interpretations of the difference between prior and new knowledge and of the resulting CC problems consequently align with coherence theories.
DT criticisms of the failures of other educational approaches to overcoming CC-related problems highlight approaches that insufficiently help students bridge prior and new knowledge (e.g., conventional transmissive approaches; Arievitch & Stetsenko, 2000; Davydov 1972/1999) and approaches that insufficiently make understandable the discontinuity between prior and new knowledge by relying primarily on students’ prior knowledge or self-directed reasoning, including constructivist educational approaches (Cobb et al., 1996; Davydov, 1972/1999; Giest & Lompscher, 2003; Karpov, 2003; Schmittau, 2004). I will show that DT approaches provide strong educational guidance through specific learning tasks, which are designed and sequenced to make students understand unambiguously one specific theoretical meaning (Davydov, 1972/1999; El’konin, 1975; Gal’perin, 1974/1989c). This contrasts with the tendency of constructivist educational approaches, which are not necessarily related to CC research, to stimulate primarily students’ own interpretations and negotiations of meaning by relying primarily on their self-directed reasoning, own experience, or familiar preinstructional modes of thinking (Cobb et al., 1996; Giest & Lompscher, 2003; Karpov, 2003; Schmittau, 2004).
Educational Recommendations to Foster CC from a DT Perspective
Methods for Relating Prior and New Knowledge
Design Education Based on Delineating the Core Conceptual Interrelations of a Subject Matter. DT approaches are characterized by the specific type of analysis of the content of theoretical knowledge after which they design education. Theoretical knowledge is defined by the theoretical mode of thinking that its content requires: explaining – via specific causal-logical relationships – the origin, genesis, and functioning of various concrete phenomena or objects based on a set of concepts systematically interrelated. The objective of supporting students to develop theoretical thinking requires the delineation of this set of core conceptual interrelations (Davydov, 1972/1999; Gal’perin, 1969/1989a, 1978/1992). This intrinsically implies delineating the theoretical thinking required to reflect on these fundamental conceptual interrelations. Davydov (1972/1999) recommended delineating the most general and fundamental conceptual interrelation, which he called a germ cell, out of which a series of objects, phenomena, or events are systematically derived and interconnected in a subject area or problem field. For instance, in mathematics, the concept of real number is based on the fundamental interrelation between a quantity and a unit of measurement (Kilpatrick et al., 1975). Delineating the set of core interrelations in a subject matter requires epistemological and logical analysis and, in Davydov’s (1972/1999) approach, paying particular attention to how they have emerged and developed in a discipline. This content analysis principle provides a general orientation to educational design even if it may not always be entirely feasible for different reasons, including (a) the complexity of the analysis (Arievitch & Stetsenko, 2000); (b) ongoing inter- and intra-disciplinary debates about what is considered the core conceptual interrelations in certain subject areas (Giest & Lompscher, 2003); and (c) the possibility of different, equally valid core conceptual interrelations in a subject area (diSessa, 1980).
Design Learning Tasks for Students to Learn, From the Outset, the Core Conceptual Interrelations. DT approaches are designed such that, from the outset, students learn especially through specific problem-solving tasks as well as through other learning tasks to engage in reasoning that best enables them to discover, reflect on, and progressively master the core conceptual interrelations. Thus, from the start, students become familiar with the conceptual interrelations required to think theoretically in a subject area or problem field. The operations to undertake in these learning tasks may be shown by the teacher first, possibly preceded by some notions explicitly taught, or directly done by the students (collectively or alone) under the guidance of the teacher, depending on the academic knowledge, the student’s level of development, and their existing knowledge.
Draw on Both Continuities and Discontinuities Between Prior and New Knowledge. To develop theoretical thinking, DT approaches aim to ensure that students adequately relate prior and new knowledge (Arievitch & Haenen, 2005; Davydov, 1972/1999; Hedegaard & Chaiklin, 2005). DT approaches draw on both continuities and discontinuities between prior and new knowledge, in accordance with their view that prior and new knowledge is discrepant but must be bridged. On the one hand, DT researchers advised confronting students to the prior knowledge that they are expected to spontaneously rely on in a problem situation, but that is inadequate to address the problem, for instance, by making them encounter an unexpected aspect of a familiar phenomenon (Davydov, 1972/1999; Gal’perin, 1978/1992). The goal is not primarily to reveal and replace misconceptions, as advocated in ontological theory. The goal, shared by framework theorists (Haenen et al., 2003; Kozulin, 2003), is to reveal the insufficiency of students’ existing knowledge to solve a type of problem and induce the need for the new theoretical knowledge to highlight the specificity of the theoretical knowledge (Davydov, 1972/1999; Galperin, 1978/1992; Giest & Lompscher, 2003; Karpov, 2013). On the other hand, DT researchers design learning tasks that strategically start from real-world problems that are relatable to students’ existing knowledge and that, therefore, must be meaningful to them in some way (Davydov, 1972/1999; Gal’perin, 1978/1992). These problems should motivate students to solve them, which may require thinking about what might interest them, depending on their age and living conditions.
Moreover, DT researchers use throughout the learning process some of students’ existing cognitive capacities and knowledge as a support to facilitate and scaffold the learning of the new knowledge as seamlessly as possible, including by directly integrating and reorganizing some prior knowledge into the new academic knowledge (Davydov, 1972/1999; Gal’perin, 1969/1989a). These concerns for bridging prior and new knowledge align with fragmentation theories. Furthermore, diSessa (1980, 1982, 2018b) shares with DT researchers the concern to significantly redesign education by bridging foundational aspects of a subject matter with students’ prior productive knowledge to facilitate understanding and foster CC (in diSessa’s words, reformulate, i.e., reconceptualize the subject matter and the pedagogical way of approaching it for cognitive simplicity). For example, diSessa (1980) argued in favor of redesigning the teaching of Newtonian mechanics on the basis of ideas about flow and conservation, which are intuitively accessible to students, as an alternative to the conventional teaching that relies on agentively causal mechanisms, which are also intuitively accessible. He suggested that teaching both, with their different characteristics, could foster flexibility in understanding and CCs.
Example 1: The Newtonian Concept of Force
This example illustrates DT principles of designing education based on analyzing the core conceptual interrelations in a subject area or problem field and solving problems such that students encounter the core conceptual interrelations, their necessity, and their theoretical logic. Chaiklin (2002) designed his upper secondary physics courses on Newtonian mechanics for 17- and 18-year-olds by first analyzing the most central problem in understanding the meaning of force: to explain why a constant motion changes (e.g., speeds up, slows down), i.e., to “explain changes in the distance that an object displaces for a given time unit” (p. 173). However, as Chaiklin expected, in line with most CC research on the topic, “most pupils come with an idea that force must be the cause of motion. It is, therefore, difficult for them to acquire the Newtonian conception of force as a cause of changes in an object’s rate of displacement” (p. 173).
To provide a basis for approaching the meaning of force, Chaiklin assumed that using a graph is the only way to describe a position for every moment of time. Indeed, Newton’s analysis assumes that moving bodies are homogeneous (ignoring the physical shapes of objects), making it possible to treat an object as if its mass was concentrated in a single point, thereby enabling one to describe its motion in one dimension with a graph. Chaiklin noted that his students already knew from previous school years how to produce and interpret graphs with two continuous variables, thus building upon their existing knowledge and abilities. He strategically started the lessons with a problem that led his students to draw conclusions about the necessity of studying motion in one dimension. He asked them, “Can you describe a movement so that others can reproduce the same movement exactly without having seen the original movement?” (p. 174). After group discussions and reflections on the problems, “the pupils had come up with the idea that studying a motion in one dimension might solve the problem (…) unlike typical teaching approaches – where pupils object to the seeming artificiality and irrelevance of one-dimensional motion – this class was actually grateful and excited about the idea of working with one-dimensional motion, because they saw the possibility of being able to solve the original problem” (p. 174).
To describe motion in one dimension, the students proposed “an experiment in which they would drop a weight attached to a strip of paper which could be marked with a spark timer (thereby registering position over time)” (p. 174). After conducting the experiment, students began to understand the relationship between a graph of displacement and the physical phenomenon it describes. Then, Chaiklin asked them “where the observer is in relation to the graph” (p. 176) to introduce the idea of “frame of reference,” “to initiate a new round of investigations that will elaborate the class’s understanding of the description of motion in a way needed for understanding the necessity of the concept of force. The formulation of this question was possible because the subject matter analysis gave the teacher (or planner) insight into the next conceptual step in the subject matter, which was used to generate a task that maintained a dynamic tension between the pupils’ capabilities and the demands in the subject matter” (p. 177).
Methods for Mastering the New Knowledge
Modeling the Theoretical Knowledge. DT approaches require the use of visual aids that reflect and model the core conceptual interrelations to help their generalization, abstraction, and mastery and to develop systematic model-based theoretical thinking. In El’konin-Davydov’s approach, a visual model is elaborated through learning tasks and represents the most fundamental conceptual interrelation or germ cell in a subject area (Davydov, 1972/1999). When the germ cell is modeled, students learn to derive its general and particular forms and instantiations and the theoretical principles that derive from it so that they are all integrated into a unified conceptual system. This learning process, which moves from the most general conceptual interrelation to various general and particular instantiations (an ascent from the abstract to the concrete, in Davydov’s terminology), helps students further master the germ cell, its explanatory potential, and limitations. The emphasis on developing knowledge transfers that account for contextual variations in order to develop systematic uses of knowledge is shared by the knowledge-in-pieces theory.
Vary the Types of Instantiation and Representation of the Core Conceptual Interrelations. The elaboration and use of the model take place through varying and contrasting the types of instantiation and representation of the core conceptual interrelations to strengthen their abstraction and generalization (Davydov, 1972/1999; Gal’perin, 1978/1992). In Gal’perin’s method of stage-by-stage formation of mental actions and concepts, learning progresses systematically by following specific stages. They are: (1) learning tasks that imply either hands-on manipulation of physical objects or their visual representations, which must, in either case, help reflect the core conceptual interrelations; (2) reasoning verbally and then internally without external support; and finally (3) mastering “purely” mental reasoning. Table 2 summarizes the CC challenges in education and educational recommendations to overcome them from a DT perspective and the divergences and convergences with the three CC research trends.
Example 2: The Concept of Real Number
This example illustrates the aforementioned educational principles in practice in mathematics. Conventional mathematics curricula in primary school usually begin with concrete teaching of arithmetic based on counting discrete objects (e.g., “How many crayons are there?”) and, through this, the properties of natural numbers. On this basis, algebra, with its abstract symbols, formulas, and unfamiliar properties of numbers (e.g., rational numbers are represented by negative numbers; decimals; or the ratio of two integers, such as −3, 0.5, or 1/2), is taught in later years. However, DT researchers and CC researchers, especially framework theorists (Christou et al., 2007; Merenluoto & Lehtinen, 2004; Vamvakoussi & Vosniadou, 2004, 2007), documented the misconceptions that result from that way of learning mathematics by enriching children’s preinstructional concepts of numbers developed in the act of counting discrete objects in everyday life (Christou et al., 2007; Vamvakoussi & Vosniadou, 2007). A misconception typically formed when learning mathematics that way is the idea that numbers have a discrete nature (i.e., there is a definite successor for each number), which interferes with the learning of rational numbers (that have a continuous nature) and algebra (with its abstract symbols and formulas and unfamiliar properties). DT mathematics lessons differ radically. They were designed to overcome these CC difficulties and to develop, by contrast, early mastery of mathematical types of thinking (Kilpatrick et al., 1975; Venenciano et al., 2021).
DT mathematics is rooted first in an analysis of the most fundamental concepts of mathematics, such as the concept of real number and its core conceptual interrelation that is at its origin: a certain quantity expressed by a unit of measurement (Arievitch & Stetsenko, 2000; Davydov, 1975a, 1975b; Gal’perin, 1969, 1989a; Karpov, 1995; Kilpatrick et al., 1975). Accordingly, from the outset, students become familiar with this core interrelation and the type of theoretical thinking that produced it. To illustrate how DT researchers designed mathematics education by relating this content analysis to students’ existing cognitive capacities and knowledge, I describe Gal’perin’s kindergarten mathematics lessons and El’konin-Davydov’s mathematics curriculum for first graders.
To introduce the concept of quantity, Gal’perin’s (1969/1989a) lessons for six-year-olds started with a demonstration of the importance of measurements in different areas of life, such as weighing objects in shops, trying on shoes, and measuring cloth. Back in the classroom, the students were invited to measure various objects: tables, windows, one another, and so on. They were asked, “What shall we measure with?” (p. 34). They subsequently realized that objects have different properties and that each object must be measured with its own measure, such as a spoon to measure water, something long to measure length, and some sort of weight to measure weight. The teacher ensured that students paid special attention to discriminating the parameter of the question asked: what is bigger, smaller, or equal? They were also taught how to measure. Initially, they measured carelessly, e.g., by leaving a space between two measurements or by measuring a segment they had already measured. When asked for their opinion about these ways of measuring, they – or the teacher – pointed out that their result would be incorrect and showed why and how. These learning tasks illustrate the DT principles of the following:
starting lessons with real-world problems (practical measurement problems in everyday life) that relate to students’ existing knowledge and motivate students to solve them,
building productively upon students’ existing cognitive abilities and knowledge (children’s abilities to roughly and sometimes erroneously compare mathematical measurement types such as length, mass, and volume),
from the outset, through specifically designed problem-solving and other learning tasks, engaging in reasoning that familiarizes students with the core conceptual interrelations and thinking (measuring quantity properties with a unit of measurement).
In addition to divisible things, the students would measure indivisible things (e.g., the length of a door), thus eliminating the discreteness of measured quantities (Gal’perin, 1969/1989a). The students, who were measuring enthusiastically, often did not notice the result they were obtaining. They, or the teacher, would point out that by using the same small object to measure, a mark could be made on the thing being measured, and the number of marks corresponded to the number of times the measurement had been applied. Students, therefore, began to “see a thing as a set of ‘the number of times a measurement was applied’” (Gal’perin, 1969/1989a, p. 35). The students then learned to compare the sets they had obtained. They were presented with a problem in this respect:
“Two rather large (15–20 pieces) and unordered groups of markers differing in only one or two elements were presented (the difference was imperceptible to the eye, and the children were unable to count). The children would then be asked whether the groups were identical or different from the others. Initially, they gave arbitrary and, of course, varied responses. But the experimenter asked, ‘How can we show who is right so that all can see it?’ If the children experienced difficulties, the experimenter would demonstrate a way to line up two (horizontal) series in a reciprocally unambiguous relation. This became the principal means for quantitative comparison of sets and, through them, magnitudes. By comparing series in this way, it was easy to teach them the ideas of ‘as much as,’ ‘equal,’ ‘more and less,’ ‘more by so much and less by so much’” (Gal’perin, 1969/1989a, p. 35–36).
On this basis, the children gradually formed an understanding and mastery of the core theoretical aspects of a real number. They understood that a unit is an abstraction, something equal to its own measure, and a number is a quantity expressed by a unit of measurement (e.g., 2 means something that is equal to two measures; Gal’perin, 1969/1989a). These learning tasks illustrate DT principles of the following:
using visual aids that help reflect the core conceptual interrelations (visual marks that indicate a number of measurements according to a unit),
varying the types of instantiation and representation of the core conceptual interrelations (measuring quantities first with various physical objects, then with symbolic visual marks, and finally with abstract theoretical reasoning),
confronting a problem where students’ preinstructional knowledge, here their usual representations of quantity, is no longer effective and even misleading (in comparing exactly two sets of measurements) to induce the need for the new theoretical knowledge and highlight its specificity (the concept of real number).
Similarly, in El’konin-Davydov’s curriculum for first graders, students were first asked to identify the physical attributes of objects that can be compared (Davydov, 1975a, 1975b). The intention was to begin lessons by appealing to children’s spontaneous curiosity about the relationships between quantities in everyday life, including comparisons, seriation, and classifications of objects, as their “practical methods of distinguishing and designating certain mathematical relationships” (Davydov, 1975a, p. 90).
Six-year-olds typically compared lengths, volumes, and masses, such as the length of one book compared to another, as Davydov (1975b) assumed. Then, they were asked to describe the relationship between the attributes of the objects being compared, e.g., the relationship between the lengths of two books placed next to each other. The students or the teacher suggested several possibilities. They named one length A and another B, e.g., then verbally said that the two lengths were not the same (in this case, they were unequal) – they used paper strips to show that one was longer. They then represented the relationships by drawing line segments (see the left side of Fig. 1).

Fig. 1
Line segments representing unequal lengths and their equalization.
Finally, they could write statements such as B > A. The students were then tasked with making unequal quantities equal, or the reverse, by adding or subtracting a length. By identifying this length, say C, they understood that to achieve equality, they must either add C to A or subtract it from B. They again represented these relationships by line segments (see the right side of Fig. 1).
Thereafter, they began to write formal equations such as B = A + C, A + C = B, B − C = A, and B − A = C. The students were subsequently asked to compare two quantities that cannot be compared directly. They were thus put in a situation where their usual representations of quantity were ineffective and misleading in representing relationships between quantities to induce the need for the concept of real number. The following quote illustrates Dougherty’s (2010) application of Davydov’s curriculum in this regard:
“To motivate that discussion (about the problem), children were given two lengths, such as the length of a bookcase and the height of a bookcase across the room. They could not move the two bookcases to make a direct comparison. They were challenged to find a way to decide if the lengths are the same, or if one is longer than the other. They decided to use an intermediary unit. That is, they made the length of one bookcase using string. They then used the string to compare it to the other length (or height). This led quite naturally to an introduction of the transitive property of equality. The children symbolically represented this as A = P, P = R, and A = R. What the children said is that if length A and length P are the same, and length P is the same as length R, then length A has to be (their emphasis) equal to length R. In this example, length P represented the intermediary unit that was used to compare one length to the other” (Dougherty, 2010, p. 66).
The lessons progressed in the same vein, with children understanding that x symbolizes an unknown quantity thanks to which “one can pass from the inequality to the equality [in equations]:
A < B
A = B − x.
x = B − A” (Davydov, 1972/1999, p. 168–169)
Finally, the most fundamental conceptual interrelation or germ cell of the concept of real number was represented in a visual symbolic model under the form of a formula, providing its explicit theorization: “A/C = N, where N is any number, A is an object represented as a quantity, and C is a unit of measure” (Davydov, 1972/1999, p. 169). Davydov’s mathematics curriculum progresses by following the DT principle that each learning step establishes, as seamlessly as possible, a systematic interrelationship with what has been previously learned so that it fits into a single conceptual system. For instance, students learn multiplication and division in direct relation to their prior familiarization with the construction and measurement of quantities, which introduces the concept of multiplicity in terms of how many times a quantity fits into what is being measured. They learn to use schematic forms such as U ||| ----→ A, which indicates that three units are used to construct or measure quantity A, or U ? ----→ A, which indicates that the student should measure the quantity A using the unit U and determine the value of? (Davydov, 1992).
Example 3: The Theory of Evolution
This example further illustrates some of the aforementioned teaching principles. Hedegaard (1996) designed lessons on the theory of evolution and collaborated with a teacher who gave these lessons to two classes of third graders (33 children aged eight to nine; with one control group of 21 children) in Denmark. Hedegaard collaborated with academic specialists to delineate the germ cell of animal evolution: the interrelation between an animal species, a population, and an ecological niche. Key examples that illustrate this most fundamental conceptual interrelation and that are relatable to the student’s prior knowledge were used as introductory real-world problems. For instance, the students were told that the Arctic hare was introduced from Norway to the Faroe Islands, where there is no snow, and after some generations, the population of Arctic hares changed color from white to brown. Different tasks and exploratory activities (e.g., identifying the living conditions of the polar bear in the Arctic after watching a film about the life of the polar bear in Greenland) and classroom discussions (e.g., students were asked “What would happen if desert animals were moved to Greenland?”) followed. Living in Denmark, the children likely already had some geographical knowledge with the examples, namely, Greenland and the Faroe Islands (both Danish protectorates). Engaged in such learning tasks, the students modeled in three steps, under the teacher’s guidance, the germ cell of the theory of animal evolution (see Fig. 2).
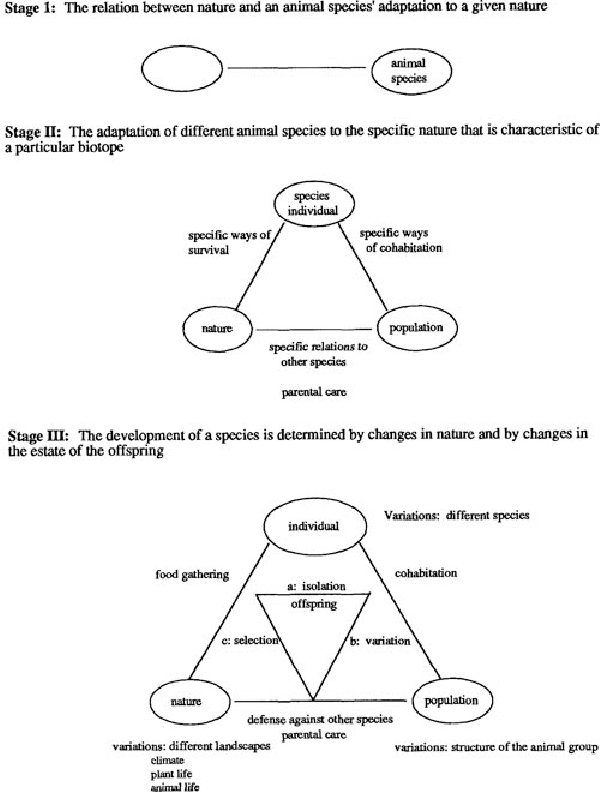
Fig. 2
Successive visual models representing core conceptual interrelations of animal evolution. Note. From “How Instruction Influences Children’s Concepts of Evolution,” by Hedegaard (1996), Mind, Culture, and Activity, 3(1), p. 14 (https://www.tandfonline.com/doi/abs/10.1207/s15327884mca0301_3). Copyright 1996 by Taylor & Francis Ltd. Reprinted with permission of Taylor & Francis.
“Stage I depicts the relationship between an animal species and its environmental conditions. Stage II depicts whether a species adapts. A species will survive if members of the population can adapt to changes in their living conditions. Stage III depicts changes in a species. New species will evolve under the following circumstances: (a) segregation and isolation of part of a population that entails change in the biotope, which involves change in the way(s) of living (ways of survival and cohabitation are important in this relation); (b) variation in the genetic material both through gene mutation and gene combination (cohabitation, parental care, and relation to other species are important for this relation); and (c) selection of offspring that have changed characteristics that are optimal relative to the environmental change (ways of survival, parental care, and defense against other species are important in this relation)” (Hedegaard, 1996, p. 14).
Hedegaard’s lessons on evolution continued in fourth-grade history courses such that the core conceptual interrelations of the animal evolution model were specified in a subsumed visual model of humans’ origin; this model itself was specified in fifth grade in a visual model of the historical change of societies (Hedegaard, 1996). This learning progression illustrates Davydov’s principle of further developing the initial germ cell and its limitations and explanatory potentials by deriving submodels, principles, and instantiations to integrate them all into a single conceptual system.
Evidence of DT Approaches’ Ability to Address Issues of CC
The available evidence on the learning outcomes of DT approaches since the 1950s shows their consistency (Arievitch & Stetsenko, 2000; Chudinova, 2019; Davydov, 1972/1999, 1988/2012; de Araujo et al., 2020; Ferreira, 2005; Gordeeva, 2020; Hedegaard & Lompscher, 1999; Karpov, 1995; Karpov & Bransford, 1995; Karpov & Haywood, 1998; Lantolf et al., 2020; Rubtsov & Ulanovskaya, 2020; Venenciano et al., 2021). It was collected in different national contexts and covered different age groups and subjects ranging from mathematics to science. This evidence has been obtained either from systematic comparative studies with control groups, from longitudinal studies (sometimes spread over several years), or from case studies. The results revealed that students consistently demonstrated a high degree of understanding, mastery of theoretical knowledge and thinking, and higher degrees of understanding than in conventional teaching. Their understanding and mastery included deeper levels of understanding, high levels of accuracy, intentional and systematic use of knowledge, far knowledge transfer, and flexible application of knowledge to new situations. Among others, model-based reasoning skills and intentional metacognitive mastery were generally emphasized. Furthermore, students’ understanding and mastery were developed earlier than in conventional education, including successful CCs, as students learned the foundations of academic knowledge earlier in different school subjects. Thus, in several areas, DT researchers have invoked this type of findings to challenge assumptions that a range of limitations in children’s comprehension abilities regarding certain CCs are inherent to developmental characteristics related to their age and experience rather than depending on the type of education received.
I briefly illustrate these claims with some of the examples described above. Hedegaard’s (1996) lessons on evolution enabled 8- and 9-year-olds to develop a high degree of mastery and systematic understanding of the core conceptual interrelation between species and ecological niches and of the temporal dimension of evolution. Other DT studies on the topic of adaptation of the living organism for 11- and 12-year-olds have found similar results (e.g., Hintz, 1984; Lompscher, 1984). This mastery included transfer to new situations directly or indirectly related to biological evolution, including historical human conditions (which were studied with systematic integration into the general model of evolution), thus indicating an integrated, flexible, and systematic model-based understanding. These degrees of systematic understanding and mastery are generally found in older educated students and are known to be difficult to achieve because of the CCs they require (Rosengren, 2012).
As another example, I explained that conventional learning of mathematics, which begins with the concrete teaching of arithmetic based on counting discrete objects, typically forms the misconception that numbers have a discrete nature. CC researchers, especially framework theorists, showed that this misconception leads to a series of related misconceptions (Christou et al., 2007; Merenluoto & Lehtinen, 2004; Vamvakoussi & Vosniadou, 2004, 2007). For example, the more digits a number has, the higher the number is; multiplication always makes the number larger; addition and subtraction are conceptualized in terms of counting; multiplication is a form of repeated addition (Vamvakoussi & Vosniadou, 2007). These misconceptions usually interfere with the learning of rational numbers and algebra, making them particularly difficult to learn, especially for children, because of the CCs it requires (rational numbers, e.g., have a continuous nature; Christou et al., 2007; Vamvakoussi & Vosniadou, 2004, 2007).
By contrast, these CC difficulties are not encountered when using DT approaches because, from the beginning, they familiarize young students with the most general and fundamental conceptual interrelations underlying real numbers, such as quantity relationships and the concept of a unit of measurement (Karpov, 1995; Kilpatrick et al., 1975; Ni & Zhou, 2005; Venenciano et al., 2021). They avoid reinforcing preconceptions about numbers as discrete. From the beginning, they also accustom students to the logic of algebraic equations. Therefore, students tend to develop an early mastery and understanding of complex mathematical concepts such as negative numbers, decimal fractions, and some algebraic reasoning (Arievitch & Stetsenko, 2000; Davydov, 1972/1999; Karpov, 1995; Venenciano et al., 2020, 2021). Specifically, after completing the mathematics lessons described above, students in kindergarten and first grade overcame the typical tendency to rely on salient superficial features of objects to evaluate quantities (a tendency that Piaget considered to be inherent in a general preoperational cognitive stage from approximately two to 6 years of age; Arievitch & Stetsenko, 2000; Davydov, 1972/1999; Gal’perin, 1978/1992; Karpov, 1995). Students indeed developed an early orientation toward discrimination and reliance on the mathematical properties of objects, including mastery of the conservation of quantity principle. More generally, DT researchers have contributed to challenging a series of supposed limitations of young children’s mathematical abilities by showing their potential capabilities in a way that has impressed the mathematical community (Venenciano et al., 2021).
Discussion
DT research and CC research have evolved without interacting with each other despite shared interests in theories of CC and related educational design. The divergences, convergences, and specificities of the approaches to CC considered here lay some foundation for overcoming this lack of interaction and suggest possibilities of articulation between DT research and CC research concerning both educational design and theories of CC. At the level of comparing DT research and CC research in general, a mutually accountable articulation is possible. CC researchers could benefit from the type of epistemological and logical analysis of academic knowledge performed in DT research to better design education. They could also question their view of academic knowledge in light of DT researchers’ characterization of academic knowledge as a set of core conceptual interrelations systematically interrelated. In turn, DT researchers aim to develop theoretical thinking in every school subject, and CC-related issues are often central to this goal. They could improve their educational design by paying attention to analyses in CC research of the types of prior knowledge that must be revised or built upon to facilitate understanding, avoid CC-related problems, and foster CCs. They could also address the fragmentation-coherence controversy to question their view of preinstructional knowledge.
At the more specific level of comparing DT research and the three CC research trends, other articulations are possible. The DT principle of designing education by delineating the core conceptual interrelations of a subject matter can complement coherence theorists’ educational strategy of first changing the prior knowledge that is assumed to systematically constrain the CC in connected or subordinate bodies of knowledge. For instance, framework theorists’ advice to first change preinstructional ideas that interfere with the understanding of gravity when teaching astronomy can complement an analysis of the core conceptual interrelations of gravity to design education. However, DT approaches could specifically enter into dialogue with knowledge-in-pieces theory concerning educational design, despite their divergences. One divergence is that DT researchers assume that preinstructional knowledge is discrepant with new academic knowledge, in line with coherence theories. For instance, diSessa (2018b) designed mathematics of motion for sixth graders that directly build upon the intuitive understanding of motion in a discrete form. By contrast, DT researchers considered that building upon students’ preinstructional understanding of discreteness in mathematics reinforces related preinstructional misconceptions and impairs the learning of the continuous nature of mathematics. DT approaches partly involve directly refining some prior knowledge into new academic knowledge but mostly use prior knowledge more indirectly than in fragmentation approaches. However, both approaches consider it crucial to use prior productive knowledge to scaffold learning. Specifically, DT researchers and diSessa share the concern to significantly redesign education by bridging foundational aspects of a subject matter with students’ prior productive knowledge to facilitate understanding and foster CC. Thus, further research could discuss the plausibility and practicality of those two different approaches or, perhaps more fruitfully, work on their mutual articulation.
Conclusion
DT research is absent from CC literature. However, DT researchers have developed specific theoretical views on CC and educational recommendations to foster CC. Available evidence suggests that DT approaches are promising for addressing CC challenges. Thus, while designing educational methods to address CC challenges is an area of research that still requires refinement, and while specific shortcomings in facilitating CC have been highlighted in different educational approaches, the alternatives offered by DT approaches deserve attention. Moreover, a series of possible articulations between DT research and CC research could contribute to refining theories of CC and related educational design.
Acknowledgments
I would like to warmly thank Professors Andrea diSessa and Seth Chaiklin for their valuable feedback on an earlier version of this paper.
Statement of Ethics
No ethical approval was required for the preparation of the manuscript, as no human or animal subjects were used.
Conflict of Interest Statement
The author has no conflicts of interest to declare.
Funding Sources
No external funding was received for the manuscript.
Author Contributions
Thomas Gennen wrote the paper.
References
- 2. Amin T. G., Levrini O. (Eds.). (2018Converging perspectives on conceptual change: Mapping an emerging paradigm in the learning sciencesRoutledge
- 4. Arievitch I. M., Haenen J. P. P. 2005 Connecting sociocultural theory and educational practice: Gal’perin’s approach Educ Psychol 40 3 155–165
- 5. Arievitch I. M., Stetsenko A. 2000 The quality of cultural tools and cognitive development: Gal’perin’s perspective and its implications Hum Dev 43 2 69–92
- 6. Arievitch I. M., van der Veer R. 1995 Furthering the internalization debate: gal’perin’s contribution Hum Dev 38 2 113–126
- 7. Bozhovich L. I., Zinchenko P. I. 1979 The psychology of acquiring factual knowledge by schoolchildren Sov Psychol 18 2 67–83. (Original work published 1941).
- 8. Carey S. 2009 The origin of concepts Oxford University Press
- 9. Chaiklin S. 2002 A Developmental teaching approach to schooling. In G. Wells, G. Claxton (Eds.), Learning for life in the 21st century (pp. 167–180Blackwell Publishing Ltd.
- 10. Chaiklin S. 2015 The concept of learning in a cultural-historical perspective. In D. Scott, E. Hargreaves (Eds.), The SAGE Handbook of Learning (pp. 94–106SAGE Publications Ltd.
- 13. Chi M. T. H. 2005 Commonsense conceptions of emergent processes: Why some misconceptions are robust J Learn Sci 14 2 161–199
- 14. Chi M. T. H. 2013 Two kinds and four sub-types of misconceived knowledge, ways to change it, and the learning outcomes. In S. Vosniadou (Ed.), International handbook of research on conceptual change2nd ed., pp. 49–70Routledge.
- 15. Chi M. T. H., Feltovich P. J., Glaser R. 1981 Categorization and representation of physics problems by experts and novices Cognit Sci 5 2 121–152
- 16. Chi M. T. H., Roscoe R. D. 2002 The processes and challenges of conceptual change. In M. Limón, L. Mason (Eds.), Reconsidering conceptual change: Issues in theory and practice (pp. 3–28Kluwer Academic Publishers.
- 17. Chi M. T. H., Roscoe R. D., Slotta J. D., Roy M., Chase C. C. 2012 Misconceived causal explanations for emergent processes Cognit Sci 36 1 1–61
- 18. Chinn C. A. 2018 Modeling, explanation, argumentation, and conceptual change. In T. G. Amin, O. Levrini (Eds.), Converging perspectives on conceptual change: Mapping an emerging paradigm in the learning sciencesRoutledge
- 20. Chudinova E. V. 2019 New biology” and its educational outcomes Psychol Sci Education 24 3 63–73
- 21. Clement J. 2013 Roles for explanatory models and analogies. In S. Vosniadou (Ed.), International handbook of conceptual change research2nd ed., pp. 412–446Routledge.
- 22. Cobb P., Perlwitz M., Underwood D. 1996 Constructivism and Activity Theory: A consideration of their similarities and differences as they relate to mathematics education. In H. Mansfield, N. A. Pateman, N. Bednarz (Eds.), Mathematics for tomorrow’s young childrenVol. 16Springer.
- 28. de Araujo G. C., Miguel J. C., Solovieva Y. 2020 Cultural-historical psychology: Contributions of developmental education in different international contexts [Special issue] Front Psychol 12
- 29. diSessa A. A. 1980 Momentum flow as an alternative perspective in elementary mechanics Am J Phys 48 5 365–369
- 30. diSessa A. A. 1982 Unlearning Aristotelian physics: a study of knowledge‐based learning Cognit Sci 6 1 37–75
- 31. diSessa A. A. 1993 Toward an epistemology of physics Cognition & Instruction 10 2 105–225
- 32. diSessa A. A. 2013 A bird’s‐eye view of the “pieces” vs. “coherence” controversy (from the “pieces” side of the fence). In S. Vosniadou (Ed.), International handbook of conceptual change research2nd ed., pp. 43–60Routledge.
- 33. diSessa A. A. 2014 A history of conceptual change research: Threads and fault lines. In R. K. Sawyer (Ed.), The cambridge handbook of the learning sciences2nd ed., pp. 88–108Cambridge University Press.
- 34. diSessa A. A. 2017 Conceptual change in a microcosm: Comparative learning analysis of a learning event Hum Dev 60 1 1–37
- 35. diSessa A. A. 2018a A friendly introduction to “knowledge in pieces”: Modeling types of knowledge and their roles in learning. In G. Kaiser, H. Forgasz, M. Graven, A. Kuzniak, E. Simmt, B. Xu (Eds.), Invited Lectures from the 13th International Congress on Mathematical Education (pp. 65–84Springer.
- 36. diSessa A. A. 2018b Computational literacy and “the big picture” concerning computers in mathematics education Math Think Learn 20 3–31 1
- 40. El’konin D. B. 1999 On the theory of primary education J Russ East Eur Psychol 37 6 71–83. (Original work published 1963).
- 41. Engeness I. 2021 Tools and signs in massive open online courses: Implications for learning and design Hum Dev 65 4 221–233
- 42. Engeness I., Lund A. 2020 Reprint of learning for the future: Insights arising from the contributions of Piotr Gal’perin to the cultural-historical theory Learn Cult Soc Interaction 25).
- 44. Engeström Y., Sannino A. 2020 From mediated actions to heterogenous coalitions : Four generations of activity-theoretical studies of work and learning Mind Cult Activ 1–20
- 46. Gal’perin P. Y. 1989a Study of the intellectual development of the child Sov Psychol 27 3 26–44. (Original work published 1969).
- 47. Gal’perin P. Y. 1989b Mental actions as a basis for the formation of thoughts and images Sov Psychol 27 3 45–64. (Original work published 1957).
- 48. Gal’perin P. Y. 1989c Organization of mental activity and the effectiveness of learning Sov Psychol 27 3 65–82. (Original work published 1974).
- 49. Gal’perin P. Y. 1992 Stage-by-stage formation as a method of psychological investigation J Russ East Eur Psychol 30 4 60–80. (Original work published 1978).
- 50. Giest H., Lompscher J. 2003 Formation of learning activity and theoretical thinking in science teaching. In A. Kozulin, B. Gindis, V.S. Ageyev, S.M. Miller (Eds.), Vygotsky’s educational theory in cultural context (pp. 267–288Cambridge University Press.
- 51. Gopnik A., Wellman H. 1994 The theory theory. In L. A. Hirschfeld, S. A. Gelman (Eds.), Mapping the mind: Domain specificity in cognition and culture (pp. 257–293Cambridge University Press.
- 52. Gordeeva T. O. 2020 Cognitive and educational effects of the El’konin-Davydov system of developmental education: Opportunities and limitations Cultural-Historical Psychol 16 4 14–25
- 53. Haenen J. 2000 Gal’perian instruction in the ZPD Hum Dev 43 2 93–98
- 54. Haenen J. 2001 Outlining the teaching–learning process: Piotr Gal’perin’s contribution Learn InStruct 11 2 157–170
- 55. Haenen J., Schrijnemakers H., Stufkens J. 2003 Sociocultural theory and the practice of teaching historical concepts. In A. Kozulin, B. Gindis, V.S. Ageyev, S.M. Miller (Eds.), Vygotsky’s educational theory in cultural context (pp. 246–266Cambridge University Press.
- 56. Hedegaard M. 1996 How instruction influences children’s concepts of evolution Mind Cult Activ 3 1 11–24
- 59. Henderson J. B., Langbeheim E., Chi M. T. H. 2018 Addressing robust misconceptions through the ontological distinction between sequential and emergent processes. In T. G. Amin, O. Levrini (Eds.), Converging perspectives on conceptual change: Mapping an emerging paradigm in the learning sciences (pp. 26–33Routledge.
- 61. Karpov Y. V. 1995 L.S. Vygotsky as a founder of a new approach to instruction Sch Psychol Int 16 2 131–142
- 62. Karpov Y. V. 2003 Vygotsky’s doctrine of scientific concepts: Its role for contemporary education. In A. Kozulin, B. Gindis, V. S. Ageyev, S. M. Miller (Eds.), Vygotsky’s Educational Theory in Cultural Context (pp. 65–82Cambridge University Press.
- 63. Karpov Y. V. 2013 A way to Implement the Neo-Vygotskian theoretical learning approach in the schools Int J Pedagogical Innov 1 1 25–35
- 64. Karpov Y. V., Bransford J. D. 1995 L.S. Vygotsky and the doctrine of empirical and theoretical learning Educ Psychol 30 2 61–66
- 65. Karpov Y. V., Haywood H. C. 1998 Two ways to elaborate Vygotsky’s concept of mediation Am Psychol 53 1 27–36
- 66. Karpov Y. V., Kozulin A. (Eds.), (2018The Vygotskian approach to teaching: Practical applications around the globe [Special issue]J Cognit Educ Psychol173
- 68. Kirschner P. A. 2009 Epistemology or pedagogy, that is the question. In S. Tobias, T. M. Duffy (Eds.), Constructivist instruction: Success or failure? (pp. 144–157Routledge.
- 69. Kirschner P. A., Sweller J., Clark R. E. 2006 Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching Educ Psychol 41 2 75–86
- 70. Kozulin A. 2003 Psychological tools and mediated learning. In A. Kozulin, B. Gindis, V.S. Ageyev, S.M. Miller (Eds.), Vygotsky’s educational theory in cultural context (pp. 15–38Cambridge University Press.
- 71. Kozulin A., Gindis B., Ageyev V.S., Miller S.M. 2003 Vygotsky’s educational theory in cultural context Cambridge University Press
- 72. Kyriakopoulou N., Vosniadou S. 2020 Theory of mind, personal epistemology, and science learning: Exploring common conceptual components Front Psychol 11 1140
- 73. Lantolf J. P., Poehner M. E. 2014 Sociocultural theory and the pedagogical imperative in L2 education: Vygotskian praxis and the research/practice divide Routledge
- 74. Lantolf J. P., Xi J., Minakova V. 2020 Sociocultural theory and concept-based language instruction Lang Teach 1 16 327–342
- 76. Levrini O., Tasquier G., Amin T. G., Branchetti L., Levin M. (Eds.), (2021Engaging with contemporary challenges through Science Education Research: Selected papers from the ESERA 2019 conference9Springer.
- 77. Limón M., Mason L. 2002 Reconsidering conceptual change: Issues in theory and practice Kluwer Academic Publishers
- 80. Margolis A. A. 2020 Zone of proximal development, scaffolding and teaching practice Cultural-Historical Psychol 16 3 15–26
- 82. Mayer R. E. 2002 Understanding conceptual change: A commentary. In M. Limón, L. Mason (Eds.), Reconsidering Conceptual Change: Issues in Theory and Practice (pp. 101–111Kluwer Academic Publishers.
- 83. Merenluoto K., Lehtinen E. 2004 Number concept and conceptual change: Towards a systemic model of the processes of change Learn InStruct 14 5 519–534
- 84. Ni Y., Zhou Y.D. 2005 Teaching and learning fraction and rational numbers: The origins and implications of whole number bias Educ Psychol 40 1 27–52
- 85. Palincsar A. S. 1998 Social constructivist perspectives on teaching and learning Ann Rev Psychol 49 345–375
- 87. Rosengren K. S. (Ed.), (2012Evolution challenges: Integrating research and practice in teaching and learning of evolutionOxford University Press
- 88. Rubtsov V. V., Ulanovskaya I. M. 2020 Learning аctivity as an effective way to develop meta-subject and personal competencies in elementary school students Cultural-Historical Psychol 16 2 51–60
- 89. Schmittau J. 2004 Vygotskian theory and mathematics education: Resolving the conceptual-procedural dichotomy Eur J Psychol Educ 19 1 19–43
- 90. Sherin B. 2018 Elements, ensembles and dynamic constructions. In T. G. Amin, O. Levrini (Eds.), Converging perspectives on conceptual change: Mapping an emerging paradigm in the learning sciences (pp. 61–78Routledge.
- 91. Smith J. P. 3rd., diSessa A. A., Roschelle J. 1994 Misconceptions reconceived: A constructivist analysis of knowledge in transition J Learn Sci 3 2 115–163
- 93. Treagust D. F., Duit R. 2008 Conceptual change: A discussion of theoretical, methodological and practical challenges for science education Cult Stud Sci Educ 3 2 297–328
- 94. Treagust D. F., Won M., McLure F. 2018 Multiple representations and students’ conceptual change in science. In T. G. Amin, O. Levrini (Eds.), Converging perspectives on conceptual change: Mapping an emerging paradigm in the learning sciences (pp. 121–128Routledge.
- 95. Vamvakoussi X., Vosniadou S. 2004 Understanding the structure of the set of rational numbers: A conceptual change approach Learn InStruct 14 5 453–467
- 97. Venenciano L. C. H., Yagi S. L., Zenigami F. K., Dougherty B. J. 2020 Supporting the development of early algebraic thinking, an alternative approach to number Invest Math Learn 12 1 38–52
- 99. Vosniadou S. 1994 Capturing and modeling the process of conceptual change Learn InStruct 4 1 45–69
- 100. Vosniadou S. 2007a Conceptual change and education Hum Dev 50 1 47–54
- 101. Vosniadou S. 2007b The cognitive-situative divide and the problem of conceptual change Educ Psychol 42 1 55–66
- 102. Vosniadou S. (Ed.), (2013International handbook of conceptual change research2nd ed.Routledge.
- 103. Vosniadou S. 2019 The development of students’ understanding of science Front Education 4 32
- 105. Vosniadou S., Brewer W. F. 1992 Mental models of the Earth: A study of conceptual change in childhood Cognit Psychol 24 4 535–585
- 106. Vosniadou S., Ioannides C., Dimitrakopoulou A., Papademetriou E. 2001 Designing learning environments to promote conceptual change in science Learn InStruct 11 4–5 381–419
- 107. Vosniadou S., Skopeliti I. 2014 Conceptual change from the framework theory side of the fence Sci Educ 23 7 1427–1445
- 109. Wagner J.F. 2006 Transfer in pieces Cognit InStruct 24 1 1–71
- 110. Zuckerman G. 2004 Development of reflection through learning activity Eur J Psychol Educ 19 1 9–18
- 1. Aidarova L. 1982 Child development and education (L. Lezhneva, Trans.). Progress.
- 3. Amineh R. J., Asl H. D. 2015 Review of Constructivism and social constructivism J Soc Sci Lit Languages 1 9–16.
- 11. Chaiklin S., Hedegaard M., Jensen U. J. 1999 Activity theory and social practice Aarhus University Press.
- 12. Chi M. T. H. 1992 Conceptual change within and across ontological categories: Examples from learning and discovery in science. In F. Giere (Ed.), Cognitive models of science (pp. 129–160University of Minnesota Press.
- 19. Christou K. P., Vosniadou S., Vamvakoussi V. 2007 Students’ interpretations of literal symbols in algebra. In S. Vosniadou, A. Baltas, X. Vamvakoussi (Eds.), Reframing the conceptual change approach in learning and instruction (pp. 283–298Elsevier.
- 23. Davydov V. V. 1975a Logical and psychological problems of elementary mathematics as an academic subject (A. Bigelow, Trans.). In J. Kilpatrick, L. P. Steffe, S. P. Clarkson, M. G. Kantowski, J. W. Wilson (Eds.), Soviet studies in the psychology of learning and teaching mathematics: Children’s capacity for learning mathematicsVol. 7, pp. 55–107).
- 24. Davydov V. V. 1975b The psychological characteristics of the “prenumerical” period of mathematics instruction (A. Bigelow, Trans.). In J. Kilpatrick, L. P. Steffe, S. P. Clarkson, M. G. Kantowski, J. W. Wilson (Eds.), Soviet studies in the psychology of learning and teaching mathematics: Children’s capacity for learning mathematicsVol. 7, pp. 109–205).
- 25. Davydov V. V. 1992 The psychological analysis of multiplication procedures Focus Learn Probl Math 14 1 3–67.
- 26. Davydov V. V. 1999 Types of generalization in instruction: Logical and psychological problems in the structuring of school curricula J. Teller Trans.) Soviet Studies in Mathematics Education (Vol. 2). (Original work published 1972).
- 27. Davydov V. V. 2012 Problems of developmental instruction: A theoretical and experimental psychological study (P. Moxhay, Trans.) Nova Science Publishers. (Original work published 1988).
- 37. Dougherty B. J. 2010 A Davydov approach to early mathematics. In Z. Usiskin, K. Andersen, N. Zotto (Eds.), Future curricular trends in school algebra and geometry: Conference proceedingsInformation Age Publishing.
- 38. El’konin D. B. 1975 Primary schoolchildren’s intellectual capabilities and the content of instruction. In J. Kilpatrick, L. P. Steffe, S. P. Clarkson, M. G. Kantowski, J. W. Wilson (Eds.), Soviet studies in the psychology of learning and teaching mathematics: Children’s capacity for learning mathematicsVol. 7, pp. 13–54).
- 39. El’konin D. B. 1989 Izbrannyje psichologicheskiye trudy [Selected Works in Psychology] Pedagogika.
- 43. Engeström Y., Miettinen R., Punamäki RL. 1999 Perspectives on activity theory Cambridge University Press.
- 45. Ferreira M. M. 2005 A Concept-based approach to writing instruction: From the abstract concept to the performance of concrete[Doctoral dissertation, The Pennsylvania State University]. Pennsylvania State Electronic Theses and Dissertations for Graduate School.
- 57. Hedegaard M., Chaiklin S. 2005 Radical-local teaching and learning: A cultural-historical approach Aarhus University Press.
- 58. Hedegaard M., Lompscher, J. (Eds.), (1999Learning activity and developmentAarhus University Press.
- 60. Hintz G. 1984 Ausbildung der Lerntätigkeit im Biologieunterricht der 5. Klasse nach der Methodedes Aufsteigen von Abstracrten zum Konkreten Die Akademie der Pedagogischen Wissenschaften der DDR. [Development of learning activity in fifth-grade biology, following the method of moving from the abstract to the concrete [unpublished doctoral dissertation].
- 67. Kilpatrick J., Steffe L. P., Clarkson S. P., Kantowski M. G., Wilson J. W. (Eds.), (1975Soviet studies in the psychology of learning and teaching mathematicsChildren’s capacity for learning mathematicsVol. 7).
- 75. Lave J., Wenger E. 1991 Situated learning: Legitimate peripheral participation Cambridge University Press.
- 78. Lompscher J. 1984 Problems and results of experimental research on the formation of theoretical thinking through instruction. In M. Hedegaard, P. Hakkarainen, Y. Engeström (Eds.), Learning and teaching on a scientific basis: Methodological and epistemological aspects of the activity theory of learning and teaching (pp. 293–357Aarhus University Press.
- 79. Ilyenkov E. 1982 The dialectics of the abstract & the concrete in Marx’s Capital. (S. Kuzyakov, Trans.) Progress Publishers. (Original work published 1960).
- 81. Markova A.K., Vale M., Trans, & Sharpe M.E. 1979 Teaching and mastering language. (Original work published in 1974).
- 86. Rogoff B. 1990 Apprenticeship in thinking: Cognitive development in social context Oxford University Press.
- 92. Talyzina N. F. 1981 The psychology of learning: theories of learning and programmed instruction. Progress. (Original work published 1975).
- 96. Vamvakoussi X., Vosniadou S. 2007 How many numbers are there in a rational numbers interval? Constraints, synthetic models and the effect of the number line. In S. Vosniadou, A. Baltas, X. Vamvakoussi (Eds.), Reframing the conceptual change approach in learning and instruction (pp. 265–282Elsevier.
- 98. Venenciano L., Polotskaia E., Mellone M., Radford L. (Eds.), (2021Davydov’s approach in the 21st century: Views from multiple perspectives [Special issue]Educ Stud Math1063
- 104. Vosniadou S., Baltas A., Vamvakoussi X. 2007 Reframing the conceptual change approach in learning and instruction (pp. 265–282Elsevier.
- 108. Vygotsky L.S. 1987 Thinking and speech (N. Minick, Trans.). In R.W. Rieber, A.S. Carton (Eds.), The collected works of L. S. Vygotsky. Problems of general psychologyVol. 1; pp. 39–285Plenum Press. (Original work published 1934).