Introduction
Mendelian randomization (MR) has become an increasingly popular tool for inferring causal relationships in the health sciences, to enable the formulation of effective health-promotion and disease-prevention strategies. MR leverages genetic data to overcome the critical issue of unmeasured confounding in using observational data for causal inference (see Box 1). The proliferation of genome-wide association studies (GWAS) on a wide range of traits and health outcomes has fuelled a boom in MR studies. However, the validity of MR depends on critical assumptions which are difficult to ensure. Thus, while the testing of a wide array of exposure-outcome pairs offers an exciting opportunity for etiological discoveries, there is also a serious risk that uncritical application will generate numerous invalid causal inferences and lead to confusion rather than clarity.
Box 1. Classic MR in a nutshell
In this review, we first provide a brief history of MR, followed by an overview of its principles, key assumptions, and statistical methodology, as well as its major limitations and recent methodological developments aimed at addressing these limitations. We give three examples to illustrate how MR has been used in psychiatric research, and conclude with a discussion of future research directions, including the integration of MR with multi-omics data and the use of MR in deciphering the complex causal networks of risk factors and disorders.
Causal inference and instrumental variable analysis
The randomized controlled trial (RCT) is widely regarded as the gold standard for establishing causality (Fisher, , ) but is often expensive, impractical, or unethical in humans. Thus, in mental health and across other fields, researchers have relied heavily on observational studies for testing causal relationships. However, causal inference from observational data is subject to multiple sources of bias, including unmeasured confounders, colliders, and non-random sampling. While there were early attempts at causal inference from observational data, such as the work by John Snow and others on the link between cholera outbreaks and the water supply in mid-19th century London (Davey Smith, ), formal statistical methodologies were not developed until the 1920s, when Sewall Wright developed path analysis in population genetics to test alternative causal models with correlations derived from observational data (Wright, ; see also Pearl, ; Stock & Trebbi, ). Later, Bradford Hill proposed empirical criteria to evaluate putative causal relationships from observational studies (Doll & Hill, ; Hill, ). Over time, multiple causal inference frameworks have been developed, including the Potential Outcome (aka. Counterfactual) framework (Rubin, ; Splawa-Neyman, Dabrowska, & Speed, ), the Campbell Causal Model (Campbell, ), the Sufficient-Component Cause model (Rothman, ), and the Causal Graph (aka. Bayesian Network) framework (Pearl, ).
Derived from path analysis, instrumental variable (IV) analysis is an important tool for causal inference. Wright (, p. 312) conceived of IV when he suggested introducing additional variables ‘which (A) affect demand conditions without affecting cost conditions or which (B) affect cost conditions without affecting demand conditions’ to overcome the difficulties in estimating supply and demand elasticities. By its nature, an IV is unlikely to affect the outcome other than through its influence on the putative exposure. An example is cigarette sales tax, which is unlikely to affect health outcomes other than through its effect on smoking behavior. Identifying a valid IV is critical, as noted by Wright (, p.314): ‘Success with this method depends on success in discovering factors of type A and B’.
In IV analysis, the causal effect of an exposure on an outcome is estimated by the ratio of two regression coefficients: the outcome regressed on the IV and the exposure regressed on the IV (Durbin, ). IV estimation has evolved to incorporate information from multiple instruments (Basmann, ; James & Singh, ; Theil, ), to use data from different samples (Angrist & Krueger, , ; Inoue & Solon, ), and for binary outcomes (Foster, ; Palmer et al., ). Since the 1990s IV analysis has been applied to economics, clinical trials, and public health (Angrist, Imbens, & Rubin, ; Imbens & Angrist, ). A landmark study used birthdate as IV to study the impact of schooling on income in countries where students must have reached a certain age at the start of their first academic year; the rationale being that children born soon after the beginning of an academic year would start school at a later age and receive less compulsory education than children born later in the academic year (Angrist & Keueger, ). Other notable applications used treatment assignment as IV to allow for non-compliance in estimating treatment effect in clinical trials (Greenland, ; Robins & Greenland, ), and cigarette tax as an IV for maternal smoking to investigate its effect on fetal health (Ringel & Evans, ).
Beginnings and expansion of MR
Decades before MR was introduced, Fisher (, p.7) recognized the value of genetic information in causal inference, drawing parallels between Mendelian segregation during meiosis and randomization in RCTs:
‘The different genotypes possible from the same mating have been beautifully randomized by the meiotic process. A more perfect control of conditions is scarcely possible, than that of different genotypes appearing in the same litter.’
Katan () was the first to propose using a genetic marker (APOE gene variants), as a proxy for a phenotype (serum cholesterol) to investigate its underlying causal relationship with another, statistically correlated, phenotype (cancer). Gray and Wheatley () coined the term ‘Mendelian Randomization’ when studying sibling bone marrow transplants for the treatment of leukemia. Later, Davey Smith and Ebrahim (, ) popularized the concept of MR in a causal inference context, showing how the parent–offspring design is more analog to the RCT than population-based cohort or case–control association studies, while recognizing the generally greater statistical power of the latter. Eventually, MR was recognized as being equivalent to IV analysis using genetic instruments (Didelez & Sheehan, ; Lawlor, Harbord, Sterne, Timpson, & Davey Smith, ; Wehby, Ohsfeldt, & Murray, ).
Early MR analyses used individual-level data on single candidate variants. Today, MR is usually applied to GWAS summary statistics, where the exposure and outcome are typically measured in different samples. The rapid growth of MR applications is spurred by three factors: widespread data sharing from published GWASs, the rise of MR methods requiring only summary statistics, and the availability of convenient software packages. A simple PubMed search using relevant keywords (Fig. 1) shows a surge in psychiatry-related MR publications since 2010. While two-sample MR takes advantage of the growth of GWASs on specific phenotypes, one-sample MR is making a resurgence with the advent of large-scale cohorts with measures on multiple phenotypes (e.g. the UK Biobank), which offer analytic possibilities not available from single-phenotype summary statistics, such as Bayesian causal network analysis (Howey, Shin, Relton, Davey Smith, & Cordell, ).
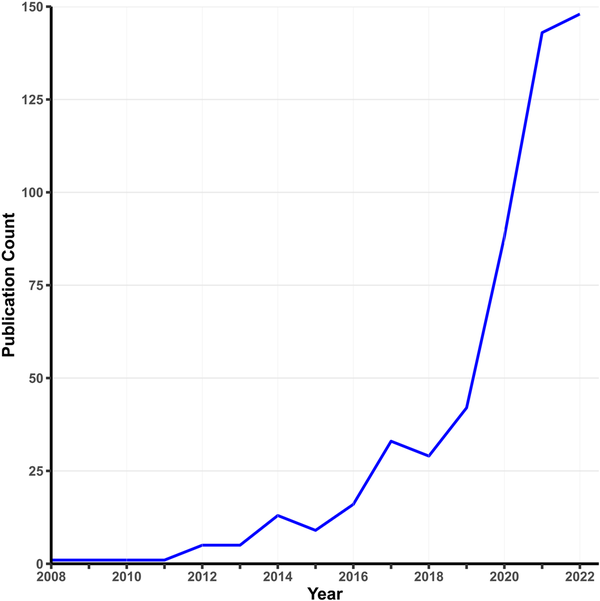
Figure 1
Growth in MR studies related to psychiatry.
Note. This figure shows the number of publications per year indexed by PubMed using the search terms ‘Mendelian randomization’ OR ‘Mendelian randomization’ AND ‘psychiatry’ as of January 2023.
Classic MR methodology
MR is often conceptualized as nature's RCT, where Mendel's laws of segregation and independent assortment provide ‘random assignment’ of alternative exposures to individual subjects. In meiosis, the two haplotypes at a locus are randomly distributed to two daughter gametes. Thus, genotypes formed by the union of parental gametes are unlikely to be associated with confounders in a randomly mating population. Reverse causation from phenotype to genotype is also unlikely since the germline genotype is fixed at conception and most genetic variation is inherited rather than acquired. Genetic variants are thus strong candidates to be used as IV (for a review, see Richmond and Smith, ).
Fundamental assumptions
MR leverages genetic instruments (GIVs) to make causal inferences. As illustrated in Fig. 2, a valid GIV needs to satisfy three assumptions (Didelez & Sheehan, ):
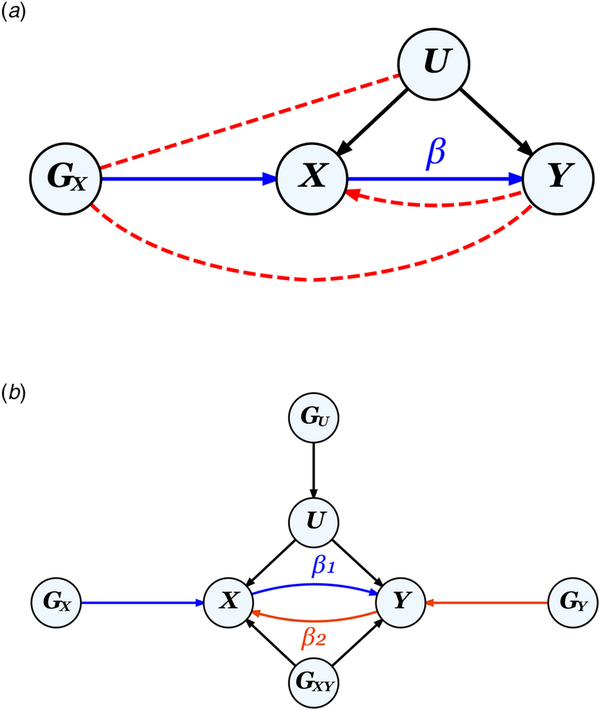
Figure 2
The MR framework and assumptions.
Note.
a. Diagram for classic MR that aims to estimate the causal effect of exposure X on outcome Y using a genetic instrument GX to control for any unmeasured confounders U, illustrating the three MR assumptions: ① relevance: GX is strongly associated with X (the blue path), ② independence: Gx is not correlated with U, and ③ exclusion restriction: GX is not correlated with Y except through X. Assumptions ② and ③ (absence of the red dotted paths) together ensure that the correlation between GX and Y can be entirely attributed to their direct relationships with X. The presence of a feedback loop, indicated by the red dotted arrow from Y to X, can bias causal effect estimates, but only when a causal effect is present.
b. Diagram for bidirectional MR on two phenotypes X and Y, where GU and GXY represent pleiotropic SNPs which would violate assumptions ② and ③ respectively, if used as genetic instruments for either X or Y. GX and GY, when uncorrelated with both GU and GXY, represent valid instruments for X and Y, respectively.
① Relevance assumption: GIV is associated with the exposure.
② Independence assumption: GIV is independent of any confounder.
③ Exclusion restriction: GIV is independent of the outcome except through the exposure.
A valid GIV is usually thought of as being causal for the exposure, but a SNP in very high linkage disequilibrium (LD) with a causal SNP could also constitute a valid instrument.
Causal effect estimation
Conceptually, the diagram in Fig. 2a implies that the effect of GIV on Y (βGY) is equal to the effect of GIV on X (βGX) multiplied by the effect of X on Y (βXY). Rearranging the equation to solve for βXY gives the simple IV ratio estimator (Durbin, ):
, where the denominator and numerator are obtained from two separate regression analyses. An alternative approach is two-stage least squares (2SLS), which first regresses X on GIV, followed by a second regression of Y on the predicted X based on the first regression (Basmann, ; Theil, ). In a single-GIV one-sample scenario, these two approaches are equivalent (Inoue & Solon, ).
When there are multiple independent GIVs, the ratio estimator can be applied to each GIV; the resulting multiple estimates can then be combined in various ways analogous to meta-analysis. Estimates can be combined most simply by inverse variance weighting (IVW), where each estimate is weighted by the inverse of its sampling variance divided by the sum of these inverses across GIVs (Burgess, Butterworth, & Thompson, ). Instead of taking a weighted mean, some have proposed taking a weighted median (Bowden, Davey Smith, Haycock, & Burgess, ) or weighted mode (Hartwig, Davey Smith, & Bowden, ) of the ratio estimates to reduce the influence of outliers arising from invalid GIVs or genotyping errors. The IVW method is equivalent to a weighted meta-regression of the GIV-outcome associations on GIV-exposure associations through the origin. While these approaches only require GWAS summary statistics, 2SLS requires individual-level data but can include GIVs that are in LD (Angrist & Krueger, ). When applied directly to a multi-GIV two-sample setting, 2SLS tends to produce more precise estimates than the generalized ratio estimator (TSIV) (Inoue & Solon, ). An extended IVW method accounts for LD by leveraging external reference panel information, providing a summary data counterpart to 2SLS (Burgess, Davies, & Thompson, ). Bowden et al. () have discussed the subtle differences between various approaches. Other statistical approaches have been proposed for IV and MR analyses, including limited information maximum likelihood (LIML; Anderson & Rubin, ; Fuller, ), Bayesian models, and semi-parametric methods (see Boehm & Zhou, ; Burgess, Small, & Thompson, for statistical reviews).
Limitations of MR
Invalid instruments
The inclusion of invalid GIVs violating one or more of the three assumptions illustrated in Fig. 2 can lead to biased causal estimates. The relevance assumption requires that the GIV-exposure association is genuine rather than a chance finding or spurious association. The exclusion restriction is violated when the GIV has a direct pleiotropic effect on the outcome, or when a SNP in LD with the GIV directly affects the outcome (Davey Smith & Ebrahim, ). Finally, the independence assumption is violated when the GIV is associated with both exposure and outcome through a confounder.
In general, MR is invalidated by biased associations from either the exposure or the outcome GWAS. Despite extensive quality control and stringent statistical corrections, residual artifacts in GWAS are still present. Population stratification is a common violator of the relevance assumption by producing non-random placement of the GIVs and the outcome in the environment. Other factors, such as cryptic relatedness, familial effects, assortative mating, and subtle batch differences in genotyping calls, can also cause biased association estimates. For instance, multi-center GWAS samples might be subject to granular population differences in the distributions of exposure, outcome, and SNP allele frequency (Brumpton et al., ). Familial effects such as genetic nurture, where parents exert an effect on offspring's phenotype through the shared environment (Bates et al., ; Kong et al., ; Tubbs, Porsch, Cherny, & Sham, ), and assortative mating, which introduces a genetic correlation between parents (Robinson et al., ; Young, Benonisdottir, Przeworski, & Kong, ), can also cause biased association estimates. Other potential sources of bias include genotyping errors, phenotype classification or measurement errors, gene–environment interaction (VanderWeele, Tchetgen Tchetgen, Cornelis, & Kraft, ), participant overlap across GWAS studies (Burgess et al., ), selection bias arising from unrepresentative sampling or differential participation (Gkatzionis & Burgess, ; Munafò & Smith, ; Munafò, Tilling, Taylor, Evans, & Smith, ; Pirastu et al., ), and survival bias due to competing risk before recruitment (Schooling et al., ).
Although MR is often assumed to be immune to bias due to reverse causation, since it utilizes genetic instruments fixed at conception, several situations may still introduce bias due to reverse causation. Burgess, Swanson, & Labrecque () discuss three such situations: when the true causal exposure is upstream to the putative exposure, the presence of feedback loops, and cross-generational effects. The biasing effect of feedback loops is not often considered when conducting MR, even though many bi-directional MR studies have identified significant effects in both directions. One proposed solution to allow for feedback loops in MR estimation procedures is to utilize structural equation modeling (Zheng et al., ).
Pleiotropy
Pleiotropy refers to the situation where one SNP affects multiple traits. It is ubiquitous in human complex traits (see Solovieff, Cotsapas, Lee, Purcell, and Smoller, for a review), with over 90% of trait-associated loci, 80% of associated genes, and 60% of associated SNPs discovered by GWAS being pleiotropic across multiple traits (Watanabe et al., ). For psychiatric disorders, pleiotropy is pervasive, with few risk alleles that are specific to a single diagnostic category (O'Donovan & Owen, ), resulting in widespread genetic correlations across disorders (Cross-Disorder Group of the Psychiatric Genomics, ). Horizontal pleiotropy, where a SNP directly influences multiple phenotypes, gives rise to invalid GIVs (Davey Smith & Hemani, ; Verbanck, Chen, Neale, & Do, ). MR Egger was introduced to allow for horizontal pleiotropy but is not valid when the pleiotropic effects on exposure and outcome are correlated due to common biological mechanisms linking the GIVs to the exposure and outcome (Morrison, Knoblauch, Marcus, Stephens, & He, ). Thus, even if MR researchers have access to well-executed and adequately powered GWAS, pleiotropy remains a challenging issue.
Weak instruments
The estimation accuracy and statistical power of MR depend on the strength of the GIV-exposure association (Brion, Shakhbazov, & Visscher, ; Burgess, ; Freeman, Cowling, & Schooling, ). Weak GIVs can lead to significant small-sample bias and unstable estimates in MR (from having a close-to-zero denominator in the ratio), known as ‘weak instrument bias’ (Bound, Jaeger, & Baker, ; Hahn & Hausman, ; Staiger & Stock, ). In general, one-sample MR causal estimates are biased toward residual exposure-outcome association from unmeasured confounders (Burgess & Thompson, ), whereas two-sample estimates are biased toward the null (Angrist & Krueger, ; Lawlor, ). Having many weak GIVs increases the variation in causal effect estimates across GIVs; such heterogeneity can be tested by an adapted Cochran's Q statistic and allowed for by modifying the weights in IVW estimation (Bowden et al., ).
Winner's curse
Selecting significant SNPs from an exposure GWAS as GIVs and using the same GWAS to obtain GIV-exposure association estimates can lead to an upward bias of these estimates, known as the ‘winner's curse’ (Kraft, ; Xiao & Boehnke, ), and result in biased MR estimates (Davey Smith & Hemani, ; Lawlor, ). Winner's curse bias is most severe in underpowered GWAS of highly polygenic phenotypes and remains non-negligible at the typical sample sizes of current GWAS. In two-sample MR without sample overlap, the GIV-outcome association estimates are not subject to the winner's curse, causing the ratio estimates to be biased toward the null (Deng, Zhang, Song, & Yu, ). However, when there is sample overlap between exposure and outcome GWAS, phenotypic correlation between exposure and outcome may introduce winner's curse bias to SNP-outcome associations, possibly resulting in false-positive causal inferences (Minelli et al., ). To avoid winner's curse, GIVs should ideally be selected a priori based on existing knowledge or a preliminary independent GWAS on the exposure (Burgess et al., ).
Recent methodological developments in MR
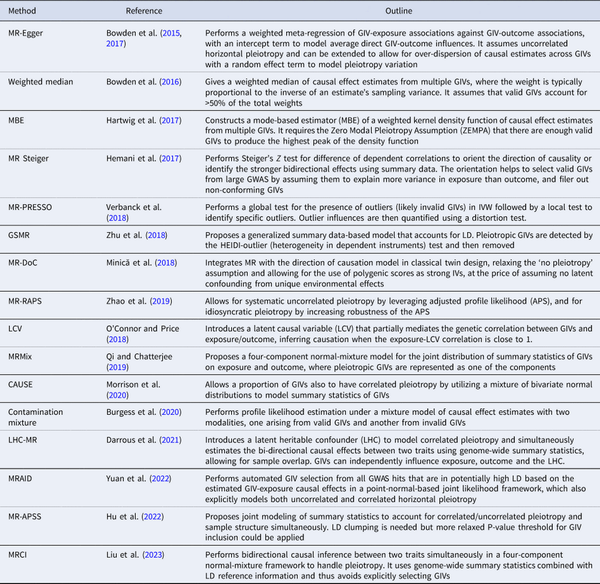
MR has traditionally been used to evaluate the causality of candidate risk factors for specific health outcomes, such as HDL for heart disease and vitamin D for type-2 diabetes. However, the recent trend of using MR more exploratively on GWAS summary statistics has increased the risk of false causal inferences due to multiple testing and the limitations mentioned above. This has motivated methodological developments which aim to improve the robustness and statistical power of MR. These methods address issues such as identifying invalid GIVs due to pleiotropy, adjusting for weak GIVs, accounting for measurement errors, and correcting for sample overlap, ‘winner's curse’, and selection bias. A selection of these methods is summarized in Table 1 (see Sanderson et al., for a review).
Addressing widespread pleiotropy
Recent methodological advancements have focused on reducing biases caused by widespread pleiotropy in complex phenotypes. Common approaches include weighting schemes, identifying and then removing pleiotropic GIVs, leveraging gene-by-environment (G × E) interactions, or explicitly modeling GIV-outcome pleiotropic effects.
IVW produces consistent MR estimates only when the pleiotropic effects of invalid GIVs on the outcome are uncorrelated with their effects on exposure (the InSIDE assumption) and have an average of zero. MR-Egger adds an intercept term to the weighted meta-regression to capture non-zero average pleiotropic effects (Bowden, Davey Smith, & Burgess, ; Burgess & Thompson, ) and can model the heterogeneity of pleiotropic effects by introducing a random effect, but still depends on the InSIDE assumption for valid causal inference (Bowden et al., ). Methods based on the identification and exclusion of GIVs with outlying causal effect estimates include Cochran's Q statistics (Bowden et al., ), MR-PRESSO (Verbanck et al., ), and GSMR (Zhu et al., ).
The presence of an interacting covariate that modifies the effect of GIV on exposure offers an opportunity for detecting and adjusting for pleiotropy, since there is a covariate value at which the GIV has no effect on exposure, so that the GIV-outcome association at this covariate value would estimate pleiotropy. When the interacting covariate is measured, MR-GxE estimates the causal effect by the regression coefficient of GIV-outcome associations on GIV-exposure associations, across different observed values of the covariate (Spiller, Slichter, Bowden, & Davey Smith, ). When it is not measured, MR-GENIUS leverages the heteroscedasticity induced by the G × E to estimate the causal effect on exposure on outcome (Tchetgen, Sun, & Walter, ). However, MR-G × E assumes that all pleiotropic effects of GIVs on outcome are independent of the covariate, while MR-GENIUS involves even stronger assumptions (Spiller, Hartwig, Sanderson, Davey Smith, & Bowden, ).
Some recent MR methods explicitly model and control for correlated horizontal pleiotropy. LCV (O'Connor & Price, ) introduces a latent causal mediator that links GIVs to both exposure and outcome, and infers an exposure-outcome causation when the latent causal mediator is almost perfectly correlated with the exposure. MRMix (Qi & Chatterjee, ) and contamination mixture (Burgess, Foley, Allara, Staley, & Howson, ) assume a normal mixture model to allow for pleiotropic SNPs among selected GIVs; the latter was found to outperform other existing methods in simulations (Slob & Burgess, ). In contrast, CAUSE (Morrison et al., ) models correlated pleiotropy across all SNPs after LD pruning, whilst MRAID (Yuan et al., ) includes all GWAS hits that are in LD and enables automatic GIV selection. Three recent methods, LHC-MR (Darrous, Mounier, & Kutalik, ), MR-APSS (Hu et al., ), and MRCI (Liu et al., ), account for sample overlap (between exposure and outcome GWAS) as well as correlated pleiotropy, by adopting an structural equation model (SEM) with a latent heritable confounder, a mixture foreground-background model, and a mixture bi-directional causation model, respectively. MR-APSS requires the selection of nearly independent GIVs, whereas LHC-MR and MRCI use all available SNPs. Since different methods have their own strengths and weaknesses, researchers often apply multiple analytic approaches to the same dataset to assess the strength of evidence for causality based on the consistency of results.
Addressing other limitations
Progress has also been made in addressing other limitations beyond horizontal pleiotropy. To reduce weak instrument bias, early approaches include selecting variants with F statistic > 10, controlling for covariates, and combining data from multiple studies (Burgess et al., ; Burgess & Thompson, ). Another approach involves combining multiple weak GIVs into a single, stronger GIV by polygenic scoring (Burgess, Dudbridge, & Thompson, ). However, polygenic scores are prone to include pleiotropic GIVs and violate MR assumptions. Modified weights in an IVW framework (Bowden et al., ) and weighted meta-regression (Cai, Hartley, Mahmoud, Tilling, & Dudbridge, ) are alternative ways for ameliorating the bias introduced by multiple weak GIVs. MR-RAPS (Zhao, Wang, Hemani, Bowden, & Small, ) is another method for robust inference that first screens out extremely weak GIVs, and then down-weights the contributions of the remaining weak GIVs.
As GWAS sample size increases, and with some phenotypes having large measurement errors, there is increasing risk of selecting instruments that are primarily associated with outcome rather than exposure. Since a valid GIV should correlate more strongly with exposure than outcome, the Steiger Z test has been proposed to orientate causation direction between phenotypes and filter out invalid GIVs (Hemani, Tilling, & Smith, ).
To address the winner's curse bias, prior statistical adjustment of GIV-exposure association statistics (e.g. MRlap by Mounier & Kutalik, ) or explicit modeling by their joint distribution with GIV-outcome association statistics (e.g. MRCI; Liu et al., ) have been suggested.
Genetic nurture stemming from correlated offspring genotypes and family environment can be addressed by directly estimating causal maternal effects on offspring phenotypes (Evans, Moen, Hwang, Lawlor, & Warrington, ). Family-based genetic association data (e.g. from parent–offspring trio or sibship designs) can be leveraged to account for assortative mating, population stratification, familial effects, and horizontal pleiotropy in MR studies (Brumpton et al., ; Davies et al., ). Typically, within-family association is free from many of the potential biases of association studies on unrelated individuals (Hwang, Davies, Warrington, & Evans, ), which may explain the often reported smaller effect size estimates from family-based association studies (Howe et al., ). Recent advances in integrating MR with the direction of causation modeling in the classical twin design have enabled the use of polygenic scores as strong IVs to improve causal effect estimation in a unidirectional (MR-DoC; Minică, Dolan, Boomsma, de Geus, & Neale, ) and bidirectional setting (MR-DoC2; Castro-de-Araujo et al., ).
Standard MR uses average causal effect estimates across population strata or interacting risk factors. Recent methods such as the residual collider-stratified approach Coscia et al. () take account of such cross-group heterogeneity when predicting the effect of altering an exposure in an individual.
MR best practices
Clinicians and applied researchers should be aware of the benefits and limitations of MR, which deserve scrutiny given the importance of causal inference for mechanistic understanding, clinical practice, and wider policy recommendations. Davies, Holmes, and Smith () and Burgess et al. () provide excellent guidelines geared toward clinicians, with checklists for assessing MR studies. Researchers should follow established quality control pipelines to address metadata errors or analytical issues (Haycock et al., ). Agreement between multiple MR analyses using various methodologies, combined with triangulation of other relevant experimental (e.g. RCT), epidemiological, or genetic evidence (e.g. colocalization), is needed strengthen the confidence in a causal finding and avoid false discoveries (see Lawlor, ; Sobczyk, Zheng, Smith, & Gaunt, ; Zuber et al. ).
Recent advances have encouraged the widespread application of MR. Many classical MR methods and recent developments have been integrated into convenient packages, such as the ‘MendelianRandomization’ R package (Broadbent et al., ; Yavorska & Burgess, ). The proliferation of large biobanks and GWAS consortia has provided the genetic data needed for using MR to examine the causal relations between numerous exposure-outcome pairs. For example, MRbase (Hemani et al., ) allows performing MR in a web browser by combining results across around 40 000 sets of summary statistics ranging from proteomics to brain region volumes, enabling ‘high-throughput’ research such as an MR screen for putative causes of Parkinson's disease using over 5000 GWAS datasets and compiling the results in an online repository (Noyce et al., ). Some have even adopted a hypothesis-free phenome-wide MR approach (Evans et al., ; Evans & Davey Smith, ), searching for causal effects of BMI on a wide range of phenotypes (Millard et al., ; Millard, Davies, Gaunt, Smith, & Tilling, ). However, studies examining many exposure-outcome pairs are susceptible to p-hacking and publication bias. Therefore, researchers need to employ rigorous control for multiple testing (e.g. by Bonferroni or false discovery rate adjustment) and report all results of MR tests performed regardless of significance, while journals should consider publishing null findings from rigorous studies.
The concept of gene–environment (G–E) equivalence adds complexity to interpreting positive MR results, which states that ‘changes in an exposure by either a hypothetical change in genotype or by a change in the environment should produce the same downstream effect on an outcome’ (Sanderson et al., , p. 26). It is suggested that this criterion needs to be fulfilled to assert causality, in addition to the three MR assumptions. Indeed, violation of G–E equivalence suggests that the exposure is not truly causal despite significant MR evidence, but represents a closely correlated proxy of a true cause. However, under this scenario, the GIVs are correlated with the true cause, which acts as a confounder for exposure-outcome association, violating the second MR assumption. Thus, the caveat of G–E equivalence reflects the inherent difficulties in ensuring that a significant MR result is not due to the violation of MR assumptions by a confounder that has a strong genetic correlation with the exposure. For example, while MR may support a causal effect of BMI on diabetes risk (Corbin et al., ), the true cause could be some trait with a strong genetic correlation with BMI, such as body fat (Jo & Mainous, ).
A closely related issue arises when the exposure is categorical or binary; the question being whether we should infer the exposure itself, or the genetic liability to the exposure, to be causal. Considering the genetic liability to be causal allows for the possibility that the true cause may be some unmeasured variable that has a strong genetic correlation with the exposure, rather than the exposure itself. For instance, a recent study found evidence for causal links between educational attainment (EA) and health outcomes using a within-sibship MR design, but interpreted these results with caution, citing the possible involvement of EA-correlated cognitive and non-cognitive pathways (Howe et al., ).
MR applications in psychiatry
The application of MR in psychiatry has become increasingly common (Pingault, Cecil, Murray, Munafò, & Viding, ). Saccaro, Gasparini, and Rutigliano () systematically reviewed published MR studies on schizophrenia, major depression, bipolar disorder, autism spectrum disorders, and ADHD, demonstrating the methodology, findings, and flaws in existing literature of over 50 articles. Here, we will highlight three examples: (1) using MR to examine the contentious causal relationship between cannabis use and psychosis, (2) using MR to clarify the potentially bi-directional relationship between intelligence and schizophrenia, (3) using MR to screen candidate modifiable risk factors for a causal effect on depression. These examples demonstrate the usefulness of MR in following up on myriad association findings and providing initial evidence for plausible causal risk factors that are often not conducive to a RCT.
Cannabis use and psychosis
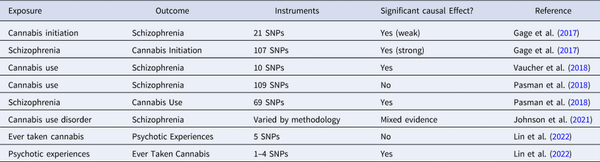
Several MR studies have been conducted to examine the controversial association between cannabis use and psychosis. Using two-sample IVW MR, Gage et al. () found evidence of a weak but significant causal effect of cannabis initiation on schizophrenia risk and a strong effect in the opposite direction. Vaucher et al. () also found significant evidence for a causal effect of ever-use of cannabis on schizophrenia risk. In contrast, Pasman et al. () found no support for a causal effect of lifetime cannabis use on schizophrenia risk but reported a strong effect in the opposite direction. Johnson et al. () used the LCV method and found no evidence of causal effect of cannabis use disorder on schizophrenia, but reached the opposite conclusion when they used multivariate MR to control for pleiotropic effects through cigarette smoking phenotypes. Using one-sample MR in the UK Biobank, B. D. Lin et al. (Lin et al. ) found evidence to support a causal effect of risk for psychosis on cannabis use, but no causal effect in the reverse direction. Together, these studies provide strong evidence of a causal link between schizophrenia and cannabis use behaviors, but only mixed evidence for a causal effect in the opposite direction. Gillespie and Kendler (), reviewing the earliest three studies along with evidence from other study designs, concluded that while there is evidence for true causality, non-causal factors such as shared genetic and familial influences and other environmental confounders also contribute to the association between cannabis use and schizophrenia. Such complexities increase the likelihood of pleiotropy and other violations of MR assumptions. In addition, the effect of cannabis use may vary depending on the pattern of use and the potency of the cannabis. Thus, future MR studies should use more nuanced definitions of cannabis use, as well as more robust study designs and analytic strategies (Table 2).
Intelligence and schizophrenia
Cognitive impairment is a core feature of schizophrenia (McCutcheon, Keefe, & McGuire, ), with premorbid intelligence consistently shown to be a strong predictor of future risk (Khandaker, Barnett, White, & Jones, ). Furthermore, schizophrenia and intelligence show strong evidence for shared genetic effects (Savage et al., ; Smeland et al., ). Three MR studies have been conducted to test for their causal links. The first used GSMR, finding statistically significant bi-directional causal relationships such that higher intelligence was protective against schizophrenia and schizophrenia leads to decreased intelligence (Savage et al., ). A subsequent study using different summary statistics for intelligence also found evidence from IVW and MR-Egger for a causal effect of higher intelligence on reduced risk for schizophrenia but did not examine the reverse causal direction (Adams, ). The most recent MR study (Ohi et al., ), which applied GSMR, found evidence that low intelligence was causally associated with schizophrenia-specific risk as well as shared schizophrenia and bipolar risk. Evidence in the reverse direction indicated that only the shared risk component is causally linked to decreasing intelligence. As opposed to the MR-based findings on cannabis use and schizophrenia, the MR evidence for a causal effect of intelligence on schizophrenia is strong and consistent. Indeed, other study designs have also supported a causal link between pre-morbid intelligence and schizophrenia (Kendler, Ohlsson, Sundquist, & Sundquist, ; Toulopoulou et al., ).
Modifiable causal risk factors for depression
MR was recently used to identify modifiable causal risk factors for depression from UK Biobank data. Out of 26 candidate risk factors, the study reported significant risk-increasing causal effects of TV use and multivitamin use, a bidirectional causal relationship between depression and daytime napping, and a protective effect of confiding in others. However, only a small number of GIVs were used in analyzing the effect of multivitamin use, and it is also unclear whether the effect of TV use is specific or related generally to media consumption/sedentary behavior. The results support the strong existing literature linking sleep dysregulation to depression (Fang, Tu, Sheng, & Shao, ; Riemann, Krone, Wulff, & Nissen, ), as well as the protective effects of social support shown by previous prospective studies (Santini, Koyanagi, Tyrovolas, Mason, & Haro, ). However, these risk factors are themselves determined by a multitude of biopsychosocial influences, and there is likely widespread pleiotropy between them and with depression, undermining the confidence in MR results. Nevertheless, if replicated by further studies employing independent samples and complementary methodologies, these findings would provide valuable insights with potential implications for the prevention and treatment of mood disorders.
Future prospects
MR is now firmly established as a powerful and rapidly advancing tool for etiological research. Two promising directions for its future development are: (1) integrating multi-omics data to elucidate the intricate biological mechanisms driving disease and disorder, and (2) generalizing its use to construct complex causal networks connecting multiple phenotypes. These developments could enable researchers to dissect mechanistic relationships, identify novel etiological pathways, and inform disease prevention and intervention efforts. Yazdani et al. () reviewed the extension from classical MR to causal networks capable of integrating large-scale omics data and provided a detailed discussion of the assumptions, identification, evaluation, and utility of causal networks.
MR with multi-omics data
Advances in multi-omic technologies have empowered the utilization of MR in exploring the causal links between molecular pathways and disease development. The possibility of mining the ‘phenome’ for disease associations was suggested by Evans et al. (), who proposed the use of GWAS to construct genome-wide allelic scores as composite proxies for numerous biological intermediate variables and to screen these scores for association with health outcomes. However, as genome-wide allelic scores are likely to have widespread effects on multiple phenotypes, they may not be ideal GIVs for MR studies (Evans et al., ; Evans & Davey Smith, ). Subsequently, transcriptome-wide association studies (TWAS) emerged, which use a regression model developed from expression quantitative trait loci (eQTL) data to impute gene expression levels from multiple SNP genotypes; the imputed expression levels of numerous genes are then analyzed for association with the phenotype (Gamazon et al., ). SMR subsequently adapted this approach into a summary statistics-based MR framework (Zhu et al., ), which was used to prioritize 55 genes whose expression levels may be causally linked to schizophrenia risk (Trubetskoy et al., ). MR-JTI (Zhou et al., ) improved upon this by incorporating multiple-tissue expression data to increase statistical power, while others have leveraged prior fine mapping to enhance MR accuracy (Zhu et al., ). Furthermore, MR is increasingly being applied to a wide range of multi-omics data, including metabolomics (Liu et al., ; Richardson et al., ), epigenetic markers (Alameda et al., ; Jamieson et al., ; Richardson et al., ), single-cell transcriptomics (Haglund et al., ), and the brain connectome (Shen et al., ; Song, Qian, Wang, Yu, & Lin, ), as exposures and/or outcomes. Omics-driven MR has the potential to provide insights into the complex biological mechanisms underlying disease occurrence.
MR and causal networks
Ultimately, MR could be used to construct causal networks of numerous environmental and biological risk factors for complex diseases across multiple inter-related phenotypes. Such a network would be extremely informative for drug repositioning and target screening, the identification of actionable clinical intervention points, and the prediction of the multiple direct and indirect consequences of any intervention.
An important development toward causal network modeling is multivariable MR (MVMR; Burgess & Thompson, ; Sanderson, Davey Smith, Windmeijer, & Bowden, ), which allows the joint estimation of the causal effects of multiple exposures on an outcome, accounting for correlated pleiotropic effects through the included exposures. MVMR was used to test the association between educational attainment and smoking after adjustment for general cognitive ability (Sanderson, Davey Smith, Bowden, & Munafò, ), and its adaptation MVMR-cML was used to assess the causal relationships between eight common cardiometabolic risk factors and coronary artery disease (Lin et al., ). However, correct causal inference in MVMR requires the selected covariates to include confounders of the exposure–outcome relationship but exclude mediators of the relationship and consequences of the outcome.
Another important development was the incorporating MR into mediation analysis (Burgess, Daniel, Butterworth, & Thompson, ; Carter et al., ; Relton & Davey Smith, ) to partition the overall causal effect of exposure X on outcome Y into direct and indirect (via measured mediator Z) components, by using GIVs for X and GIVs for Z to estimate the effects of X (on Z and Y) and the effects of Z (on Y), respectively. The data can be fitted to a pre-specified SEM of all the variables, as suggested by Sanderson (). In principle, MR-based mediation analysis can be extended to a general framework for estimating causal relationships among multiple traits, where a trait can be influenced by some variables and at the time exert influence on other variables, blurring the distinction between exposure and outcome.
An important strength of SEM methodology is its ability to include latent variables to explain phenotypic correlations among measured variables. With the development of methods such as GCTA (Lee, Yang, Goddard, Visscher, & Wray, ) and LDSC (Bulik-Sullivan et al., ) to estimate the genetic correlations (as against phenotypic correlations) of phenotype pairs using GWAS data, SEM has been extended to include latent genetic factors to explain the pattern of genetic correlations among multiple phenotypes (Genomic SEM: Grotzinger et al., ). The incorporation of latent variables into MR-based causal inference could eventually lead to a general approach for constructing and testing complex causal networks of multiple latent and measured phenotypes. In such a framework, SNP genotypes represent ‘external’ variables that help to clarify and estimate the causal relationships among the multiple phenotypes.
SEM is powerful and rigorous for comparing alternative causal models but can be unwieldy for constructing data-driven models with many measured variables. Directed acyclic graph (DAG) models, rooted in Bayesian principles, are more scalable. Typical DAG algorithms start by linking variables via their pairwise correlations, followed by eliminating non-causal links through conditional independence, and then orientate causal directions of the remaining edges using the collider and other principles. However, Bayesian causal networks have their own limitations, prompting recent efforts to integrate MR and DAG for more robust causal inference. Howey et al. () used MR-determined ‘genetic anchors’ to resolve the directionality of edges in DAGs with greater confidence. Amar, Sinnott-Armstrong, Ashley, and Rivas () proposed a method, cGAUGE, where DAG is employed to identify valid GIVs for MR, to determine causal connections in phenotype networks. DAG-based methods are better suited for large biobanks than for single-phenotype GWAS, given their requirements for raw data on both genotypes and (multiple) phenotypes from the same individuals. As standard DAGs do not permit causal loops, they fall short in capturing feedback mechanisms in real-world causal networks, which can result in symptom escalation as well as stabilization (e.g. the escalation of obesity and lack of exercise due to a vicious cycle of mutually reinforcing effects).
Conclusion
Mendelian randomization leverages genetic data to overcome the problem of unmeasured confounders in detecting and quantifying causal relationships. With easily accessible GWAS summary statistics on an ever-increasing number of diseases and traits, as well as user-friendly analytic tools, MR studies have become increasingly easy to perform. Many published studies have already applied MR to study the causes and consequences of psychiatric disorders. However, there are important limitations to consider when planning, implementing, and evaluating MR studies, to counter possible violation of assumptions which can lead to false positive causal inferences. Substantial methodological advances have been made in addressing the widespread pleiotropy observed across complex traits, but additional challenges remain. Nevertheless, MR in the multi-omics era holds great promise for elucidating some of the most pressing questions in psychiatry, and ultimately in constructing evidence-based causal networks that link biological and environmental risk factors to multiple intermediate phenotypes and psychiatric disorders. Such causal networks can generate detailed predictions of the consequences of different interventions, potentially guiding the identification of new treatment targets and the formulation of public health policies.
Acknowledgement
Funding from State Key Laboratory of Brain and Cognitive sciences, The University of Hong Kong.
References
- Adams C. D. (2020). A multivariable Mendelian randomization to appraise the pleiotropy between intelligence, education, and bipolar disorder in relation to schizophrenia. Scientific Reports, 10(1), 1–10. https://doi.org/10.1038/s41598-020-63104-6
- Alameda L., Trotta G., Quigley H., Rodriguez V., Gadelrab R., Dwir D., … Forti M. D. (2022). Can epigenetics shine a light on the biological pathways underlying major mental disorders? Psychological Medicine, 52(9), 1645–1665. https://doi.org/10.1017/S0033291721005559
- Amar D., Sinnott-Armstrong N., Ashley E. A., & Rivas M. A. (2021). Graphical analysis for phenome-wide causal discovery in genotyped population-scale biobanks. Nature Communications, 12(1), 350. https://doi.org/10.1038/s41467-020-20516-2
- Anderson T. W., & Rubin H. (1949). Estimation of the parameters of a single equation in a complete system of stochastic equations. The Annals of Mathematical Statistics, 20(1), 46–63.
- Angrist J. D., Imbens G. W., & Rubin D. B. (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association, 91(434), 444–455. https://doi.org/10.2307/2291629
- Angrist J. D., & Keueger A. B. (1991). Does compulsory school attendance affect schooling and earnings? The Quarterly Journal of Economics, 106(4), 979–1014.
- Angrist J. D., & Krueger A. B. (1992a). The effect of age at school entry on educational attainment: An application of instrumental variables with moments from two samples. Journal of the American Statistical Association, 87(418), 328–336. https://doi.org/10.1080/01621459.1992.10475212
- Angrist J. D., & Krueger A. B. (1992b). Estimating the payoff to schooling using the Vietnam-Era draft lottery. No 4067, NBER Working Papers. Cambridge, MA: National Bureau of Economic Research. https://doi.org/10.3386/w4067
- Angrist J. D., & Krueger A. B. (1995). Split-sample instrumental variables estimates of the return to schooling. Journal of Business & Economic Statistics, 13(2), 225–235. https://doi.org/10.2307/1392377
- Basmann R. L. (1957). A generalized classical method of linear-estimation of coefficients in a structural equation. Econometrica, 25(1), 77–83. https://doi.org/10.2307/1907743
- Bates T. C., Maher B. S., Medland S. E., McAloney K., Wright M. J., Hansell N. K., … Gillespie N. A. (2018). The nature of nurture: Using a virtual-parent design to test parenting effects on children's educational attainment in genotyped families. Twin Research and Human Genetics, 21(2), 73–83. https://doi.org/10.1017/thg.2018.11
- Boehm F. J., & Zhou X. (2022). Statistical methods for Mendelian randomization in genome-wide association studies: A review. Computational and Structural Biotechnology Journal, 20, 2338–2351. https://doi.org/10.1016/j.csbj.2022.05.015
- Bound J., Jaeger D. A., & Baker R. M. (1995). Problems with instrumental variables estimation when the correlation between the instruments and the endogeneous explanatory variable is weak. Journal of the American Statistical Association, 90(430), 443–450. https://doi.org/10.2307/2291055
- Bowden J., Davey Smith G., & Burgess S. (2015). Mendelian Randomization with invalid instruments: Effect estimation and bias detection through Egger regression. International Journal of Epidemiology, 44(2), 512–525. https://doi.org/10.1093/ije/dyv080
- Bowden J., Davey Smith G., Haycock P. C., & Burgess S. (2016). Consistent estimation in Mendelian randomization with some invalid instruments using a weighted median estimator. Genetic Epidemiology, 40(4), 304–314. https://doi.org/10.1002/gepi.21965
- Bowden J., Del Greco M. F., Minelli C., Davey Smith G., Sheehan N., & Thompson J. (2017). A framework for the investigation of pleiotropy in two-sample summary data Mendelian randomization. Statistics in Medicine, 36(11), 1783–1802. https://doi.org/10.1002/sim.7221
- Bowden J., Del Greco M. F., Minelli C., Zhao Q., Lawlor D. A., Sheehan N. A., … Davey Smith G. (2019). Improving the accuracy of two-sample summary-data Mendelian randomization: Moving beyond the NOME assumption. International Journal of Epidemiology, 48(3), 728–742. https://doi.org/10.1093/ije/dyy258
- Brion M. J., Shakhbazov K., & Visscher P. M. (2013). Calculating statistical power in Mendelian randomization studies. International Journal of Epidemiology, 42(5), 1497–1501. https://doi.org/10.1093/ije/dyt179
- Broadbent J. R., Foley C. N., Grant A. J., Mason A. M., Staley J. R., & Burgess S. (2020). MendelianRandomization v0.5.0: Updates to an R package for performing Mendelian randomization analyses using summarized data. Wellcome Open Research, 5, 252. https://doi.org/10.12688/wellcomeopenres.16374.2
- Brumpton B., Sanderson E., Heilbron K., Hartwig F. P., Harrison S., Vie G. Å., … The Within-family Consortium. (2020). Avoiding dynastic, assortative mating, and population stratification biases in Mendelian randomization through within-family analyses. Nature Communications, 11(1), 1–13. https://doi.org/10.1038/s41467-020-17117-4
- Bulik-Sullivan B., Loh P.-R., Finucane H. K., Ripke S., Yang J., … Neale B. M. (2015). LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nature Genetics, 47(3), 291–295. https://doi.org/10.1038/ng.3211
- Burgess S. (2014). Sample size and power calculations in Mendelian randomization with a single instrumental variable and a binary outcome. International Journal of Epidemiology, 43(3), 922–929. https://doi.org/10.1093/ije/dyu005
- Burgess S., Butterworth A., & Thompson S. G. (2013). Mendelian Randomization analysis with multiple genetic variants using summarized data. Genetic Epidemiology, 37(7), 658–665. https://doi.org/10.1002/gepi.21758
- Burgess S., Daniel R. M., Butterworth A. S., Thompson S. G., & the EPIC-InterAct Consortium. (2015). Network Mendelian randomization: Using genetic variants as instrumental variables to investigate mediation in causal pathways. International Journal of Epidemiology, 44(2), 484–495. https://doi.org/10.1093/ije/dyu176
- Burgess S., Davey Smith G., Davies N. M., Dudbridge F., Gill D., Glymour M. M., … Theodoratou E. (2019). Guidelines for performing Mendelian randomization investigations. Wellcome Open Research, 4, 186. https://doi.org/10.12688/wellcomeopenres.15555.1
- Burgess S., Davies N. M., & Thompson S. G. (2016a). Bias due to participant overlap in two-sample Mendelian randomization. Genetic Epidemiology, 40(7), 597–608. https://doi.org/10.1002/gepi.21998
- Burgess S., Dudbridge F., & Thompson S. G. (2016b). Combining information on multiple instrumental variables in Mendelian randomization: Comparison of allele score and summarized data methods. Statistics in Medicine, 35(11), 1880–1906. https://doi.org/10.1002/sim.6835
- Burgess S., Foley C. N., Allara E., Staley J. R., & Howson J. M. M. (2020). A robust and efficient method for Mendelian randomization with hundreds of genetic variants. Nature Communications, 11(1), 376. https://doi.org/10.1038/s41467-019-14156-4
- Burgess S., & Thompson S. G. (2011a). Avoiding bias from weak instruments in Mendelian randomization studies. International Journal of Epidemiology, 40(3), 755–764. https://doi.org/10.1093/ije/dyr036
- Burgess S., & Thompson S. G. (2011b). Bias in causal estimates from Mendelian randomization studies with weak instruments. Statistics in Medicine, 30(11), 1312–1323. https://doi.org/10.1002/sim.4197
- Burgess S., & Thompson S. G. (2015). Multivariable Mendelian randomization: The use of pleiotropic genetic variants to estimate causal effects. American Journal of Epidemiology, 181(4), 251–260. https://doi.org/10.1093/aje/kwu283
- Burgess S., & Thompson S. G. (2017). Interpreting findings from Mendelian randomization using the MR-egger method. European Journal of Epidemiology, 32(5), 377–389. https://doi.org/10.1007/s10654-017-0255-x
- Burgess S., Small D. S., & Thompson S. G. (2017). A review of instrumental variable estimators for Mendelian randomization. Statistical Methods in Medical Research, 26(5), 2333–2355. https://doi.org/10.1177/0962280215597579
- Burgess S., Swanson S. A., & Labrecque J. A. (2021). Are Mendelian randomization investigations immune from bias due to reverse causation? European Journal of Epidemiology, 36(3), 253–257. https://doi.org/10.1007/s10654-021-00726-8
- Cai S., Hartley A., Mahmoud O., Tilling K., & Dudbridge F. (2022). Adjusting for collider bias in genetic association studies using instrumental variable methods. Genetic Epidemiology, 46(5–6), 303–316. https://doi.org/10.1002/gepi.22455
- Campbell D. T. (1957). Factors relevant to the validity of experiments in social settings. Psychological Bulletin, 54, 297–312. https://doi.org/10.1037/h0040950
- Carter A. R., Sanderson E., Hammerton G., Richmond R. C., Davey Smith G., Heron J., … Howe L. D. (2021). Mendelian randomisation for mediation analysis: Current methods and challenges for implementation. European Journal of Epidemiology, 36(5), 465–478. https://doi.org/10.1007/s10654-021-00757-1
- Castro-de-Araujo L. F. S., Singh M., Zhou Y., Vinh P., Verhulst B., Dolan C. V., & Neale M. C. (2023). MR-DoC2: Bidirectional causal modeling with instrumental variables and data from relatives. Behavior Genetics, 53(1), 63–73. https://doi.org/10.1007/s10519-022-10122-x
- Corbin L. J., Richmond R. C., Wade K. H., Burgess S., Bowden J., Davey Smith G., & Timpson N. J. (2016). Body mass index as a modifiable risk factor for type 2 diabetes: Refining and understanding causal estimates using Mendelian randomisation. Diabetes, 65(10), 3002–3007. https://doi.org/10.2337/db16-0418
- Coscia C., Gill D., Benítez R., Pérez T., Malats N., & Burgess S. (2022). Avoiding collider bias in Mendelian randomization when performing stratified analyses. European Journal of Epidemiology, 37(7), 671–682. https://doi.org/10.1007/s10654-022-00879-0
- Cross-Disorder Group of the Psychiatric Genomics (2019). Genomic relationships, novel loci, and pleiotropic mechanisms across eight psychiatric disorders. Cell, 179(7), 1469. https://doi.org/10.1016/j.cell.2019.11.020
- Darrous L., Mounier N., & Kutalik Z. (2021). Simultaneous estimation of bi-directional causal effects and heritable confounding from GWAS summary statistics. Nature Communications, 12(1), 7274. https://doi.org/10.1038/s41467-021-26970-w
- Davey Smith G. (2002). Commentary: Behind the broad street pump: Aetiology, epidemiology and prevention of cholera in mid-19th century britain. International Journal of Epidemiology, 31(5), 920–932. https://doi.org/10.1093/ije/31.5.920
- Davey Smith G., & Ebrahim S. (2003). ‘Mendelian randomization’: Can genetic epidemiology contribute to understanding environmental determinants of disease? International Journal of Epidemiology, 32(1), 1–22. https://doi.org/10.1093/ije/dyg070
- Davey Smith G., & Ebrahim S. (2004). Mendelian randomization: Prospects, potentials, and limitations. International Journal of Epidemiology, 33(1), 30–42. https://doi.org/10.1093/ije/dyh132
- Davey Smith G., & Hemani G. (2014). Mendelian randomization: Genetic anchors for causal inference in epidemiological studies. Human Molecular Genetics, 23(R1), R89–R98. https://doi.org/10.1093/hmg/ddu328
- Davies N. M., Holmes M. V., & Smith G. D. (2018). Reading Mendelian randomisation studies: A guide, glossary, and checklist for clinicians. BMJ, 362, k601. https://doi.org/10.1136/bmj.k601
- Davies N. M., Howe L. J., Brumpton B., Havdahl A., Evans D. M., & Davey Smith G. (2019). Within family Mendelian randomization studies. Human Molecular Genetics, 28(R2), R170–R179. https://doi.org/10.1093/hmg/ddz204
- Deng L., Zhang H., Song L., & Yu K. (2020). Approximation of bias and mean-squared error in two-sample Mendelian randomization analyses. Biometrics, 76(2), 369–379. https://doi.org/10.1111/biom.13169
- Didelez V., & Sheehan N. (2007). Mendelian randomization as an instrumental variable approach to causal inference. Statistical Methods in Medical Research, 16(4), 309–330. https://doi.org/10.1177/0962280206077743
- Doll R., & Hill A. B. (1950). Smoking and carcinoma of the lung; preliminary report. British Medical Journal, 2(4682), 739–748. https://doi.org/10.1136/bmj.2.4682.739
- Durbin J. (1954). Errors in variables. Revue de l'Institut International de Statistique / Review of the International Statistical Institute, 22(1/3), 23. https://doi.org/10.2307/1401917
- Evans D. M., Brion M. J. A., Paternoster L., Kemp J. P., McMahon G., Munafò M., … Smith G. D. (2013). Mining the human phenome using allelic scores that index biological intermediates. PLOS Genetics, 9(10), e1003919. https://doi.org/10.1371/journal.pgen.1003919
- Evans D. M., & Davey Smith G. (2015). Mendelian randomization: New applications in the coming age of hypothesis-free causality. Annual Review of Genomics and Human Genetics, 16(1), 327–350. https://doi.org/10.1146/annurev-genom-090314-050016
- Evans D. M., Moen G. H., Hwang L. D., Lawlor D. A., & Warrington N. M. (2019). Elucidating the role of maternal environmental exposures on offspring health and disease using two-sample Mendelian randomization. International Journal of Epidemiology, 48(3), 861–875. https://doi.org/10.1093/ije/dyz019
- Fang H., Tu S., Sheng J., & Shao A. (2019). Depression in sleep disturbance: A review on a bidirectional relationship, mechanisms and treatment. Journal of Cellular and Molecular Medicine, 23(4), 2324–2332. https://doi.org/10.1111/jcmm.14170
- Fisher R. A. (1925). Statistical methods for research workers. Edinburgh, London: Oliver and Boyd.
- Fisher R. A. (1926). The arrangement of field experiments. Journal of the Ministry of Agriculture, 33, 503–513.
- Fisher R. A. (1952). Statistical methods in genetics. Heredity, 6(1), 1–12. https://doi.org/10.1038/hdy.1952.1
- Foster E. M. (1997). Instrumental variables for logistic regression: An illustration. Social Science Research, 26(4), 487–504. https://doi.org/10.1006/ssre.1997.0606
- Freeman G., Cowling B. J., & Schooling C. M. (2013). Power and sample size calculations for Mendelian randomization studies using one genetic instrument. International Journal of Epidemiology, 42(4), 1157–1163. https://doi.org/10.1093/ije/dyt110
- Fuller W. A. (1977). Some properties of a modification of the limited information estimator. Econometrica, 45(4), 939–953.
- Gage S. H., Jones H. J., Burgess S., Bowden J., Davey Smith G., Zammit S., & Munafò M. R. (2017). Assessing causality in associations between cannabis use and schizophrenia risk: A two-sample Mendelian randomization study. Psychological Medicine, 47(5), 971–980. https://doi.org/10.1017/S0033291716003172
- Gamazon E. R., Wheeler H. E., Shah K. P., Mozaffari S. V., Aquino-Michaels K., Carroll R. J., … Im H. K. (2015). A gene-based association method for mapping traits using reference transcriptome data. Nature Genetics, 47(9), 1091–1098. https://doi.org/10.1038/ng.3367
- Gillespie N. A., & Kendler K. S. (2021). Use of genetically informed methods to clarify the nature of the association between Cannabis use and risk for schizophrenia. JAMA Psychiatry, 78(5), 467–468. https://doi.org/10.1001/jamapsychiatry.2020.3564
- Gkatzionis A., & Burgess S. (2019). Contextualizing selection bias in Mendelian randomization: How bad is it likely to be? International Journal of Epidemiology, 48(3), 691–701. https://doi.org/10.1093/ije/dyy202
- Gray R., & Wheatley K. (1991). How to avoid bias when comparing bone marrow transplantation with chemotherapy. Bone Marrow Transplantation, 7(Suppl 3), 9–12.
- Greenland S. (2000). An introduction to instrumental variables for epidemiologists. International Journal of Epidemiology, 29(4), 722–729. https://doi.org/10.1093/ije/29.4.722
- Grotzinger A. D., Rhemtulla M., de Vlaming R., Ritchie S. J., Mallard T. T., Hill W. D., … Tucker-Drob E. M. (2019). Genomic structural equation modelling provides insights into the multivariate genetic architecture of complex traits. Nature Human Behaviour, 3(5), 513–525. https://doi.org/10.1038/s41562-019-0566-x
- Haglund A., Zuber V., Yang Y., Abouzeid M., Feleke R., Ko J. H., … Johnson M. R. (2022). Single-cell Mendelian randomisation identifies cell-type specific genetic effects on human brain disease and behaviour. bioRxiv. https://doi.org/10.1101/2022.11.28.517913
- Hahn J., & Hausman J. (2003). Weak instruments: Diagnosis and cures in empirical econometrics. The American Economic Review, 93(2), 118–125.
- Hartwig F. P., Davey Smith G., & Bowden J. (2017). Robust inference in summary data Mendelian randomization via the zero modal pleiotropy assumption. International Journal of Epidemiology, 46(6), 1985–1998. https://doi.org/10.1093/ije/dyx102
- Haycock P. C., Borges M. C., Burrows K., Lemaitre R. N., Harrison S., … Burgess S., … , Fatty Acids in Cancer Mendelian Randomization Collaboration. (2023). Design and quality control of large-scale two-sample Mendelian randomization studies. International Journal of Epidemiology, 52(5), 1498–1521. https://doi.org/10.1093/ije/dyad018
- Hemani G., Tilling K., & Smith G. D. (2017). Orienting the causal relationship between imprecisely measured traits using GWAS summary data. PLOS Genetics, 13(11), e1007081. https://doi.org/10.1371/journal.pgen.1007081
- Hemani G., Zheng J., Elsworth B., Wade K. H., Haberland V., Baird D., … Haycock P. C. (2018). The MR-base platform supports systematic causal inference across the human phenome. Elife, 7, e34408. https://doi.org/10.7554/eLife.34408
- Hill A. B. (1965). The environment and disease: Association or causation? Proceedings of the Royal Society of Medicine, 58(5), 295–300. https://doi.org/10.1177/003591576505800503
- Howe L. J., Nivard M. G., Morris T. T., Hansen A. F., Rasheed H., Cho Y., … Davies N. M. (2022). Within-sibship genome-wide association analyses decrease bias in estimates of direct genetic effects. Nature Genetics, 54(5), 581–592. https://doi.org/10.1038/s41588-022-01062-7
- Howe L. J., Rasheed H., Jones P. R., Boomsma D. I., Evans D. M., Giannelis A., … Davies N. M. (2023). Educational attainment, health outcomes and mortality: A within-sibship Mendelian randomization study. International Journal of Epidemiology, 52(5), 1579–1591. https://doi.org/10.1093/ije/dyad079
- Howey R., Shin S. Y., Relton C., Davey Smith G., & Cordell H. J. (2020). Bayesian network analysis incorporating genetic anchors complements conventional Mendelian randomization approaches for exploratory analysis of causal relationships in complex data. PLoS Genetics, 16(3), e1008198. https://doi.org/10.1371/journal.pgen.1008198
- Hu X., Zhao J., Lin Z., Wang Y., Peng H., Zhao H., … Yang C. (2022). Mendelian randomization for causal inference accounting for pleiotropy and sample structure using genome-wide summary statistics. Proceedings of the National Academy of Sciences, 119(28), e2106858119. https://doi.org/10.1073/pnas.2106858119
- Hwang L.-D., Davies N. M., Warrington N. M., & Evans D. M. (2021). Integrating family-based and Mendelian randomization designs. Cold Spring Harbor Perspectives in Medicine, 11(3), a039503. https://doi.org/10.1101/cshperspect.a039503
- Imbens G. W., & Angrist J. D. (1994). Identification and estimation of local average treatment effects. Econometrica, 62(2), 467–475. https://doi.org/10.2307/2951620
- Inoue A., & Solon G. (2010). Two-sample instrumental variables estimators. The Review of Economics and Statistics, 92(3), 557–561. https://doi.org/10.1162/REST_a_00011
- James L. R., & Singh B. K. (1978). An introduction to the logic, assumptions, and basic analytic procedures of two-stage least squares. Psychological Bulletin, 85, 1104–1122. https://doi.org/10.1037/0033-2909.85.5.1104
- Jamieson E., Korologou-Linden R., Wootton R. E., Guyatt A. L., Battram T., Burrows K., … Richmond R. C. (2020). Smoking, DNA methylation, and lung function: A mendelian randomization analysis to investigate causal pathways. The American Journal of Human Genetics, 106(3), 315–326. https://doi.org/10.1016/j.ajhg.2020.01.015
- Jo A., & Mainous III A. G. (2018). Informational value of percent body fat with body mass index for the risk of abnormal blood glucose: A nationally representative cross-sectional study. BMJ Open, 8(4), e019200. https://doi.org/10.1136/bmjopen-2017-019200
- Johnson E. C., Hatoum A. S., Deak J. D., Polimanti R., Murray R. M., Edenberg H. J., … Agrawal A. (2021). The relationship between cannabis and schizophrenia: A genetically informed perspective. Addiction, 116(11), 3227–3234. https://doi.org/10.1111/add.15534
- Katan M. B. (1986). Apolipoprotein E isoforms, serum cholesterol, and cancer. The Lancet, 327(8479), 507–508. https://doi.org/10.1016/S0140-6736(86)92972-7
- Kendler K. S., Ohlsson H., Sundquist J., & Sundquist K. (2015). IQ and schizophrenia in a Swedish national sample: Their causal relationship and the interaction of IQ with genetic risk. American Journal of Psychiatry, 172(3), 259–265. https://doi.org/10.1176/appi.ajp.2014.14040516
- Khandaker G. M., Barnett J. H., White I. R., & Jones P. B. (2011). A quantitative meta-analysis of population-based studies of premorbid intelligence and schizophrenia. Schizophrenia Research, 132(2), 220–227. https://doi.org/10.1016/j.schres.2011.06.017
- Kong A., Thorleifsson G., Frigge M. L., Vilhjalmsson B. J., Young A. I., Thorgeirsson T. E., … Stefansson K. (2018). The nature of nurture: Effects of parental genotypes. Science, 359(6374), 424–428. https://doi.org/10.1126/science.aan6877
- Kraft P. (2008). Curses – winner's and otherwise – in genetic epidemiology. Epidemiology, 19(5), 649–651, discussion 657-8. https://doi.org/10.1097/EDE.0b013e318181b865.
- Lawlor D. A. (2016). Commentary: Two-sample Mendelian randomization: Opportunities and challenges. International Journal of Epidemiology, 45(3), 908–915. https://doi.org/10.1093/ije/dyw127
- Lawlor D. A., Harbord R. M., Sterne J. A. C., Timpson N., & Davey Smith G. (2008). Mendelian randomization: Using genes as instruments for making causal inferences in epidemiology. Statistics in Medicine, 27(8), 1133–1163. https://doi.org/10.1002/sim.3034
- Lee S. H., Yang J., Goddard M. E., Visscher P. M., & Wray N. R. (2012). Estimation of pleiotropy between complex diseases using single-nucleotide polymorphism-derived genomic relationships and restricted maximum likelihood. Bioinformatics, 28(19), 2540–2542. https://doi.org/10.1093/bioinformatics/bts474
- Lin B. D., Pries L. K., Sarac H. S., van Os J., Rutten B. P. F., Luykx J., & Guloksuz S. (2022). Nongenetic factors associated with psychotic experiences among UK biobank participants: Exposome-wide analysis and mendelian randomization analysis. JAMA Psychiatry, 79(9), 857–868. https://doi.org/10.1001/jamapsychiatry.2022.1655
- Lin Z., Xue H., & Pan W. (2023). Robust multivariable Mendelian randomization based on constrained maximum likelihood. The American Journal of Human Genetics, 110(4), 592–605. https://doi.org/10.1016/j.ajhg.2023.02.014
- Liu J., van Klinken J. B., Semiz S., van Dijk K. W., Verhoeven A., Hankemeier T., … Demirkan A. (2017). A Mendelian randomization study of metabolite profiles, fasting glucose, and type 2 diabetes. Diabetes, 66(11), 2915–2926. https://doi.org/10.2337/db17-0199
- Liu Z., Qin Y., Wu T., Tubbs J. D., Baum L., Mak T. S. H., … Sham P. C. (2023). Reciprocal causation mixture model for robust Mendelian randomization analysis using genome-scale summary data. Nature Communications, 14(1), 1131. https://doi.org/10.1038/s41467-023-36490-4
- McCutcheon R. A., Keefe R. S. E., & McGuire P. K. (2023). Cognitive impairment in schizophrenia: Aetiology, pathophysiology, and treatment. Molecular Psychiatry, 28(5), 1902–1918. https://doi.org/10.1038/s41380-023-01949-9
- Millard L. A. C., Davies N. M., Gaunt T. R., Smith G. D., & Tilling K. (2018). Software application profile: PHESANT: A tool for performing automated phenome scans in UK Biobank. International Journal of Epidemiology, 47(1), 29–35. https://doi.org/10.1093/ije/dyx204
- Millard L. A. C., Davies N. M., Timpson N. J., Tilling K., Flach P. A., & Smith G. D. (2015). MR-PheWAS: Hypothesis prioritization among potential causal effects of body mass index on many outcomes, using Mendelian randomization. Scientific Reports, 5(1), 1–17. https://doi.org/10.1038/srep16645
- Minelli C., Del Greco M. F., van der Plaat D. A., Bowden J., Sheehan N. A., & Thompson J. (2021). The use of two-sample methods for Mendelian randomization analyses on single large datasets. International Journal of Epidemiology, 50(5), 1651–1659. https://doi.org/10.1093/ije/dyab084
- Minică C. C., Dolan C. V., Boomsma D. I., de Geus E., & Neale M. C. (2018). Extending causality tests with genetic instruments: An integration of mendelian randomization with the classical twin design. Behavior Genetics, 48(4), 337–349. https://doi.org/10.1007/s10519-018-9904-4
- Morrison J., Knoblauch N., Marcus J. H., Stephens M., & He X. (2020). Mendelian Randomization accounting for correlated and uncorrelated pleiotropic effects using genome-wide summary statistics. Nature Genetics, 52(7), 740–747. https://doi.org/10.1038/s41588-020-0631-4
- Mounier N., & Kutalik Z. (2023). Bias correction for inverse variance weighting Mendelian randomization. Genetic Epidemiology, 47(4), 314–331. https://doi.org/10.1101/2021.03.26.437168
- Munafò M. R., Tilling K., Taylor A. E., Evans D. M., & Smith G. D. (2018). Collider scope: When selection bias can substantially influence observed associations. International Journal of Epidemiology, 47(1), 226–235. https://doi.org/10.1093/ije/dyx206
- Munafò M., & Smith G. D. (2018). Biased estimates in Mendelian randomization studies conducted in unrepresentative samples. JAMA Cardiology, 3(2), 181. https://doi.org/10.1001/jamacardio.2017.4279
- Noyce A. J., Bandres-Ciga S., Kim J., Heilbron K., Kia D., Hemani G., … Singleton A. B. (2019). The Parkinson's disease mendelian randomization research portal. Movement Disorders: Official Journal of the Movement Disorder Society, 34(12), 1864–1872. https://doi.org/10.1002/mds.27873
- O'Connor L. J., & Price A. L. (2018). Distinguishing genetic correlation from causation across 52 diseases and complex traits. Nature Genetics, 50(12), 1728–1734. https://doi.org/10.1038/s41588-018-0255-0
- O'Donovan M. C., & Owen M. J. (2016). The implications of the shared genetics of psychiatric disorders. Nature Medicine, 22(11), 1214–1219. https://doi.org/10.1038/nm.4196
- Ohi K., Takai K., Kuramitsu A., Sugiyama S., Soda M., Kitaichi K., & Shioiri T. (2021). Causal associations of intelligence with schizophrenia and bipolar disorder: A Mendelian randomization analysis. European Psychiatry, 64(1), e61. https://doi.org/10.1192/j.eurpsy.2021.2237
- Palmer T. M., Sterne J. A., Harbord R. M., Lawlor D. A., Sheehan N. A., Meng S., … Didelez V. (2011). Instrumental variable estimation of causal risk ratios and causal odds ratios in Mendelian randomization analyses. American Journal of Epidemiology, 173(12), 1392–1403. https://doi.org/10.1093/aje/kwr026
- Pasman J. A., Verweij K. J. H., Gerring Z., Stringer S., Sanchez-Roige S., Treur J. L., … Vink J. M. (2018). GWAS of lifetime cannabis use reveals new risk loci, genetic overlap with psychiatric traits, and a causal influence of schizophrenia. Nature Neuroscience, 21(9), 1161–1170. https://doi.org/10.1038/s41593-018-0206-1
- Pearl J. (1995). Causal diagrams for empirical research. Biometrika, 82(4), 669–688. https://doi.org/10.2307/2337329
- Pearl J. (2022). Interview with Judea Pearl. Observational Studies, 8(2), 23–36. https://doi.org/10.1353/obs.2022.0007
- Pingault J.-B., Cecil C. A. M., Murray J., Munafò M. R., & Viding E. (2017). Causal inference in psychopathology: A systematic review of Mendelian randomisation studies aiming to identify environmental risk factors for psychopathology. Psychopathology Review, a4(1), 4–25. https://doi.org/10.5127/pr.038115
- Pirastu N., Cordioli M., Nandakumar P., Mignogna G., Abdellaoui A., Hollis B., … Ganna A. (2021). Genetic analyses identify widespread sex-differential participation bias. Nature Genetics, 53(5), 663–671. https://doi.org/10.1038/s41588-021-00846-7
- Qi G., & Chatterjee N. (2019). Mendelian randomization analysis using mixture models for robust and efficient estimation of causal effects. Nature Communications, 10(1), 1941. https://doi.org/10.1038/s41467-019-09432-2
- Relton C. L., & Davey Smith G. (2012). Two-step epigenetic Mendelian randomization: A strategy for establishing the causal role of epigenetic processes in pathways to disease. International Journal of Epidemiology, 41(1), 161–176. https://doi.org/10.1093/ije/dyr233
- Richardson T. G., Leyden G. M., Wang Q., Bell J. A., Elsworth B., Smith G. D., & Holmes M. V. (2022). Characterising metabolomic signatures of lipid-modifying therapies through drug target Mendelian randomisation. PLOS Biology, 20(2), e3001547. https://doi.org/10.1371/journal.pbio.3001547
- Richardson T. G., Richmond R. C., North T. L., Hemani G., Davey Smith G., Sharp G. C., & Relton C. L. (2019). An integrative approach to detect epigenetic mechanisms that putatively mediate the influence of lifestyle exposures on disease susceptibility. International Journal of Epidemiology, 48(3), 887–898. https://doi.org/10.1093/ije/dyz119
- Richmond R. C., & Smith G. D. (2022). Mendelian randomization: Concepts and scope. Cold Spring Harbor Perspectives in Medicine, 12(1), a040501. https://doi.org/10.1101/cshperspect.a040501
- Riemann D., Krone L. B., Wulff K., & Nissen C. (2020). Sleep, insomnia, and depression. Neuropsychopharmacology, 45(1), 74–89. https://doi.org/10.1038/s41386-019-0411-y
- Ringel J. S., & Evans W. N. (2001). Cigarette taxes and smoking during pregnancy. American Journal of Public Health, 91(11), 1851–1856.
- Robins J. M., & Greenland S. (1996). Identification of causal effects using instrumental variables: Comment. Journal of the American Statistical Association, 91(434), 456–458. https://doi.org/10.2307/2291630
- Robinson M. R., Kleinman A., Graff M., Vinkhuyzen A. A. E., Couper D., Miller M. B., … Visscher P. M. (2017). Genetic evidence of assortative mating in humans. Nature Human Behaviour, 1(1), 1–13. https://doi.org/10.1038/s41562-016-0016
- Rothman K. J. (1976). Causes. American Journal of Epidemiology, 104(6), 587–592. https://doi.org/10.1093/oxfordjournals.aje.a112335
- Rubin D. B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology, 66, 688–701. https://doi.org/10.1037/h0037350
- Saccaro L. F., Gasparini S., & Rutigliano G. (2022). Applications of Mendelian randomization in psychiatry: A comprehensive systematic review. Psychiatric Genetics, 32(6), 199–213. https://doi.org/10.1097/YPG.0000000000000327
- Sanderson E. (2021). Multivariable Mendelian randomization and mediation. Cold Spring Harbor Perspectives in Medicine, 11(2), a038984. https://doi.org/10.1101/cshperspect.a038984
- Sanderson E., Davey Smith G., Bowden J., & Munafò M. R. (2019a). Mendelian randomisation analysis of the effect of educational attainment and cognitive ability on smoking behaviour. Nature Communications, 10(1), 2949. https://doi.org/10.1038/s41467-019-10679-y
- Sanderson E., Davey Smith G., Windmeijer F., & Bowden J. (2019b). An examination of multivariable Mendelian randomization in the single-sample and two-sample summary data settings. International Journal of Epidemiology, 48(3), 713–727. https://doi.org/10.1093/ije/dyy262
- Sanderson E., Glymour M. M., Holmes M. V., Kang H., Morrison J., Munafò M. R., … Davey Smith G. (2022). Mendelian randomization. Nature Reviews Methods Primers, 2(1), 1–21. https://doi.org/10.1038/s43586-021-00092-5
- Santini Z. I., Koyanagi A., Tyrovolas S., Mason C., & Haro J. M. (2015). The association between social relationships and depression: A systematic review. Journal of Affective Disorders, 175, 53–65. https://doi.org/10.1016/j.jad.2014.12.049
- Savage J. E., Jansen P. R., Stringer S., Watanabe K., Bryois J., De Leeuw C. A., … Posthuma D. (2018). Genome-wide association meta-analysis in 269867 individuals identifies new genetic and functional links to intelligence. Nature Genetics, 50(7), 912–919. https://doi.org/10.1038/s41588-018-0152-6
- Schooling C. M., Lopez P. M., Yang Z., Zhao J. V., Au Yeung S. L., & Huang J. V. (2021). Use of multivariable Mendelian randomization to address biases due to competing risk before recruitment. Frontiers in Genetics, 11, 610852. https://doi.org/10.3389/fgene.2020.610852
- Shen X., Howard D. M., Adams M. J., Hill W. D., Clarke T. K., Adams M. J., … McIntosh A. M. (2020). A phenome-wide association and Mendelian randomisation study of polygenic risk for depression in UK Biobank. Nature Communications, 11(1), 2301. https://doi.org/10.1038/s41467-020-16022-0
- Slob E. A. W., & Burgess S. (2020). A comparison of robust Mendelian randomization methods using summary data. Genetic Epidemiology, 44(4), 313–329. https://doi.org/10.1002/gepi.22295
- Smeland O. B., Bahrami S., Frei O., Shadrin A., O'Connell K., Savage J., … Andreassen O. A. (2019). Genome-wide analysis reveals extensive genetic overlap between schizophrenia, bipolar disorder and intelligence. Molecular Psychiatry, 25(4), 844–853. https://doi.org/10.1038/s41380-018-0332-x
- Sobczyk M. K., Zheng J., Smith G. D., & Gaunt T. R. (2022). Systematic comparison of Mendelian randomization studies and randomized controlled trials using electronic databases (p. 2022.04.11.22273633). p. 2022.04.11.22273633. medRxiv. https://doi.org/10.1101/2022.04.11.22273633
- Solovieff N., Cotsapas C., Lee P. H., Purcell S. M., & Smoller J. W. (2013). Pleiotropy in complex traits: Challenges and strategies. Nature Reviews Genetics, 14(7), 483–495. https://doi.org/10.1038/nrg3461
- Song W., Qian W., Wang W., Yu S., & Lin G. N. (2021). Mendelian randomization studies of brain MRI yield insights into the pathogenesis of neuropsychiatric disorders. BMC Genomics, 22(Suppl 3), 342. https://doi.org/10.1186/s12864-021-07661-8
- Spiller W., Hartwig F. P., Sanderson E., Davey Smith G., & Bowden J. (2022). Interaction-based Mendelian randomization with measured and unmeasured gene-by-covariate interactions. PLoS ONE, 17(8), e0271933. https://doi.org/10.1371/journal.pone.0271933
- Spiller W., Slichter D., Bowden J., & Davey Smith G. (2019). Detecting and correcting for bias in Mendelian randomization analyses using Gene-by-Environment interactions. International Journal of Epidemiology, 48(3), 702–712. https://doi.org/10.1093/ije/dyy204
- Splawa-Neyman J., Dabrowska D. M., & Speed T. P. (1990). On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statistical Science, 5(4), 465–472.
- Staiger D., & Stock J. H. (1997). Instrumental variables regression with weak instruments. Econometrica, 65(3), 557–586. https://doi.org/10.2307/2171753
- Stock J. H., & Trebbi F. (2003). Retrospectives: Who invented instrumental variable regression? Journal of Economic Perspectives, 17(3), 177–194. https://doi.org/10.1257/089533003769204416
- Tchetgen E. T., Sun B., & Walter S. (2021). The GENIUS approach to robust mendelian randomization inference. Statistical Science, 36(3), 443–464. https://doi.org/10.1214/20-STS802
- Theil H. (1953). Repeated least squares applied to complete equation systems. The Hague: Central Planning Bureau.
- Toulopoulou T., van Haren N., Zhang X., Sham P. C., Cherny S. S., Campbell D. D., … Kahn R. S. (2015). Reciprocal causation models of cognitive vs volumetric cerebral intermediate phenotypes for schizophrenia in a pan-European twin cohort. Molecular Psychiatry, 20(11), 1386–1396. https://doi.org/10.1038/mp.2014.152
- Trubetskoy V., Pardiñas A. F., Qi T., Panagiotaropoulou G., Awasthi S., Bigdeli T. B., … O'Donovan M. C. (2022). Mapping genomic loci implicates genes and synaptic biology in schizophrenia. Nature, 604(7906), 502–508. https://doi.org/10.1038/s41586-022-04434-5
- Tubbs J. D., Porsch R. M., Cherny S. S., & Sham P. C. (2020). The genes we inherit and those we don't: Maternal genetic nurture and child BMI trajectories. Behavior Genetics, 50(5), 310–319. https://doi.org/10.1007/s10519-020-10008-w
- VanderWeele T. J., Tchetgen Tchetgen E. J., Cornelis M., & Kraft P. (2014). Methodological challenges in Mendelian randomization. Epidemiology, 25(3), 427–435. https://doi.org/10.1097/ede.0000000000000081
- Vaucher J., Keating B. J., Lasserre A. M., Gan W., Lyall D. M., Ward J., … Holmes M. V. (2018). Cannabis use and risk of schizophrenia: A Mendelian randomization study. Molecular Psychiatry, 23(5), 1287–1292. https://doi.org/10.1038/mp.2016.252
- Verbanck M., Chen C. Y., Neale B., & Do R. (2018). Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nature Genetics, 50(5), 693–698. https://doi.org/10.1038/s41588-018-0099-7
- Watanabe K., Stringer S., Frei O., Umićević Mirkov M., de Leeuw C., Polderman T. J. C., … Posthuma D. (2019). A global overview of pleiotropy and genetic architecture in complex traits. Nature Genetics, 51(9), 1339–1348. https://doi.org/10.1038/s41588-019-0481-0
- Wehby G. L., Ohsfeldt R. L., & Murray J. C. (2008). “Mendelian randomization” equals instrumental variable analysis with genetic instruments. Statistics in Medicine, 27(15), 2745–2749. https://doi.org/10.1002/sim.3255
- Wright P. G. (1928). The tariff on animal and vegetable oils. New York: Macmillan.
- Wright S. (1921). Correlation and causation. Journal of Agricultural Research, XX(7), 557–585.
- Xiao R., & Boehnke M. (2009). Quantifying and correcting for the winner's curse in genetic association studies. Genetic Epidemiology, 33(5), 453–462. https://doi.org/10.1002/gepi.20398
- Yavorska O. O., & Burgess S. (2017). Mendelian randomization: An R package for performing Mendelian randomization analyses using summarized data. International Journal of Epidemiology, 46(6), 1734–1739. https://doi.org/10.1093/ije/dyx034
- Yazdani A., Yazdani A., Mendez-Giraldez R., Samiei A., Kosorok M. R., & Schaid D. J. (2022). From classical Mendelian randomization to causal networks for systematic integration of multi-omics. Frontiers in Genetics, 13, 990486. https://doi.org/10.3389/fgene.2022.990486
- Young A. I., Benonisdottir S., Przeworski M., & Kong A. (2019). Deconstructing the sources of genotype-phenotype associations in humans. Science, 365(6460), 1396–1400. https://doi.org/10.1126/science.aax3710
- Yuan Z., Liu L., Guo P., Yan R., Xue F., & Zhou X. (2022). Likelihood-based Mendelian randomization analysis with automated instrument selection and horizontal pleiotropic modeling. Science Advances, 8(9), eabl5744. https://doi.org/10.1126/sciadv.abl5744
- Zhao Q., Wang J., Hemani G., Bowden J., & Small D. S. (2019). Statistical inference in two-sample summary-data Mendelian randomization using robust adjusted profile score. arXiv. https://doi.org/10.48550/arXiv.1801.09652
- Zheng J., Baird D., Borges M.-C., Bowden J., Hemani G., Haycock P., … Smith G. D. (2017). Recent developments in Mendelian randomization studies. Current Epidemiology Reports, 4(4), 330–345. https://doi.org/10.1007/s40471-017-0128-6
- Zhou D., Jiang Y., Zhong X., Cox N. J., Liu C., & Gamazon E. R. (2020). A unified framework for joint-tissue transcriptome-wide association and Mendelian randomization analysis. Nature Genetics, 52(11), 1239–1246. https://doi.org/10.1038/s41588-020-0706-2
- Zhu A., Matoba N., Wilson E. P., Tapia A. L., Li Y., Ibrahim J. G., … Love M. I. (2021). MRLocus: Identifying causal genes mediating a trait through Bayesian estimation of allelic heterogeneity. PLoS Genetics, 17(4), e1009455. https://doi.org/10.1371/journal.pgen.1009455
- Zhu Z., Zhang F., Hu H., Bakshi A., Robinson M. R., Powell J. E., … Yang J. (2016). Integration of summary data from GWAS and eQTL studies predicts complex trait gene targets. Nature Genetics, 48(5), 481–487. https://doi.org/10.1038/ng.3538
- Zhu Z., Zheng Z., Zhang F., Wu Y., Trzaskowski M., Maier R., … Yang J. (2018). Causal associations between risk factors and common diseases inferred from GWAS summary data. Nature Communications, 9(1), 224. https://doi.org/10.1038/s41467-017-02317-2
- Zuber V., Grinberg N. F., Gill D., Manipur I., Slob E. A. W., Patel A., … Burgess S. (2022). Combining evidence from Mendelian randomization and colocalization: Review and comparison of approaches. American Journal of Human Genetics, 109(5), 767–782. https://doi.org/10.1016/j.ajhg.2022.04.001